![]()
- 平方根
- 三平方の定理
- ブロックUIプログラミングツールでダイアログボックスを使用
- 関数を使用
今回からブロックUIプログラミングツールの上級編に入ります。
上級編のはじめは中学校の数学の範囲に合わせたプログラミングになります。
論理的な考え方のための基礎知識は初級編と中級編でそれなりについていると思われますので、プログラムのさらに深い部分に入っていきます。
数学の範囲として、「平方根」と「三平方の定理」について書いていきます。
また、ブロックUIプログラミングツールを用いてダイアログボックスを使用した対話型の計算を行っていきます。
平方根
四角形の面積は、縦と横の長さをかけて求めていました。
以下は、幅が20 高さが15の場合の長方形、幅と高さが20の正方形です。
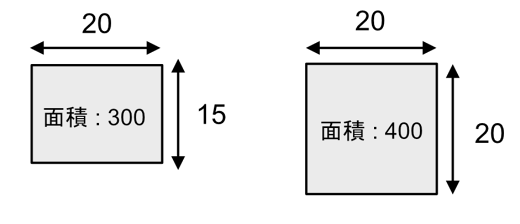
では、面積が300で幅が20で高さが分からないとした場合、高さの値は何になるでしょうか?
これは以下の公式を組み替えることで求まります。
四角形の面積 = 幅 x 高さ値を入れて組み替えると以下のようになります。
300 = 20 x 高さ
高さ = 300 ÷ 20 = 150正方形の場合も同様です。
400 = 20 x 高さ
高さ = 400 ÷ 20 = 20正方形の場合は、幅と高さは同じ長さになります。
この面積の式は「400 = 20 x 20 = 202」と置き換えできます。
公式にすると「正方形の面積 = 一辺の長さ2」となります。
この「一辺の長さ」をX、「正方形の面積」をYとして「Y = X2」のような式にした場合、
Xを求める計算は ![]() と記載できます。
と記載できます。
このときの ![]() は「ルート」と呼ばれます。
は「ルート」と呼ばれます。
ここでは便宜上「√」「√Y」のように記載します。
「ルートY」のように読みます。
二乗の計算のとき、元の値を求めるこの記述を「平方根」と呼びます。
平方根は3DCGやCADに限らずコンピュータの計算では内部的によく使われます。
コンピュータ内部では平方根はソフトウェアとしての処理ではなく、最も重要なハードウェアとなるCPU(コンピュータの頭脳に相当する部分、厳密にはFPUと呼ばれる個所が担当)内で実装されています。
コンピュータは2進数や16進数が基礎になっているため、以下はよく見る計算になります。
22 = 4
42 = 16
162 = 256
2562 = 65536
これを平方根で置き換えると、以下のようになります。
√4 = √(22) = 2
√16 = √(42) = 4
√256 = √(162) = 16
√65536 = √(2562) = 256
平方根の計算
平方根の計算は、以下のように二乗になる数を外に出すことができます。
√50 = √(25 x 2) = √(52 x 2) = 5 x √2ルート内の乗算は2つの平方根に分離できます。
√32 = √(8 x 4) = √8 x √4 = (√2 x √4) x √4 = 4 x √2ルート内の除算は2つの平方根に分離できます。
√1.5 = √15 ÷ √10平方根で覚えておいたほうがいい値
√2、√3、√5は平方根の計算ではよく出てくる値のため、結果を覚えておいた方がよいかもしれません。
これらは割り切れない数になります。
√2 = 1.41421356 (語呂合わせで「一夜一夜に人見頃(ひとよひとよにひとみごろ)」)√3 = 1.7320508(語呂合わせで「人並みに奢れや(ひとなみにおごれや)」)√5 = 2.2360679(語呂合わせで「 富士山麓オウム鳴く(ふじさんろくおうむなく)」)平方根の分解と計算
「√100」は「10」と計算ができますが、
「√10」は関数電卓を使用すると「3.1622776..」のようになります。
[問題 1] 「√10」を関数電卓を使わずに数値として計算しましょう。小数点以下5桁まで求めてそれ以下を切り捨てとします。
[答え 1] 3.16227
「√10」を分解して計算します。「√10」は「√2」と「√5」に分解できるため、上記の覚えている数値で置き換えることができます。
√10 = √2 x √5 = 1.41421356 x 2.2360679 = 3.162277545260724結果を小数点以下5桁までとした場合、「3.16227」となります。
直角三角形の1辺の長さを計算 (三平方の定理)
平方根1つだけでは何が便利なのか分かりにくいため、利用されている箇所から見ていくことにします。
以下のような直角三角形の辺の長さがA/B/C、AとBが直角とした場合、「C2 = A2 + B2」が成り立ちます。
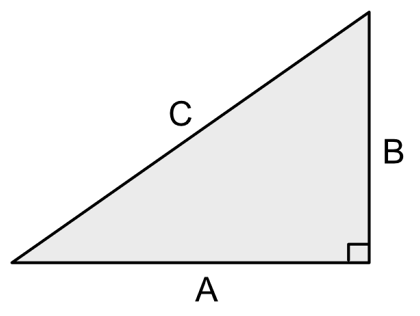
これは「三平方の定理」(ピタゴラスの定理)と呼ばれます。
では、実際に数値を入れて確認してみましょう。
[問題 2] 直角三角形の2辺が40と30であるとき、斜辺の辺Cの長さを求めましょう。
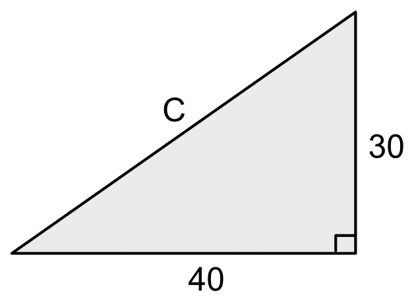
[答え 2] 50
「C2 = 402 + 302」より、「C = √(402 + 302) = √2500 = 50」となります。
二乗を展開するのに平方根を使用しました。
これは簡単な応用ですが、平方根はさまざまな式で利用されています。
ブロックUIプログラミングツールを使用して直角三角形の1辺の長さを計算
では、直角三角形の1辺の長さの計算をブロックUIプログラミングツールで実装してみましょう。
直角を構成する辺Aと辺Bは変数として入力するものとしました。
入力用のダイアログボックスを表示
ブロックUIプログラミングツールで以下のようにブロックを構成しました。
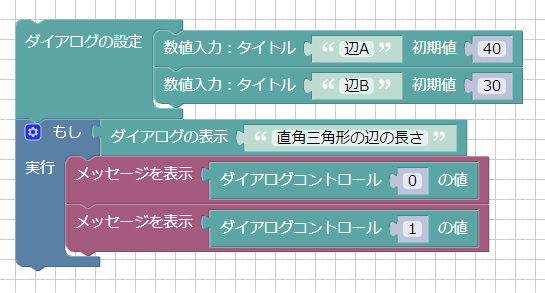
「ダイアログボックス」は、値を入力するためのユーザーインターフェース(UI)です。
これは数学ではなくコンピュータとしての単語になります。
「ユーザーインターフェース」というのは、数値や文字列を入力する際の仕組みを指します。
ブロックUIプログラミングツールで実行すると、以下のダイアログボックスが表示されます。
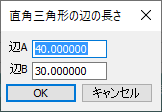
「辺A」「辺B」の入力部分の数値を指定して「OK」ボタンを押すことで、メッセージウィンドウ内に入力値の結果が出力されます。
このダイアログボックスを使用することで、「[中級] 体積の計算、変数とループ」で説明していた「入力と出力」の「入力」を変数への値の直接代入ではなく、対話型で行えるようになります。
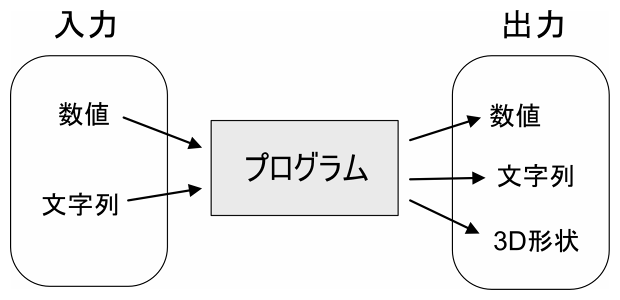
では、このダイアログボックスの作成方法を見ていきます。
ブロックUIプログラミングツールの左端のツールボックスから「UI」を選択すると、ダイアログボックスを作成するためのブロックが一覧表示されます。
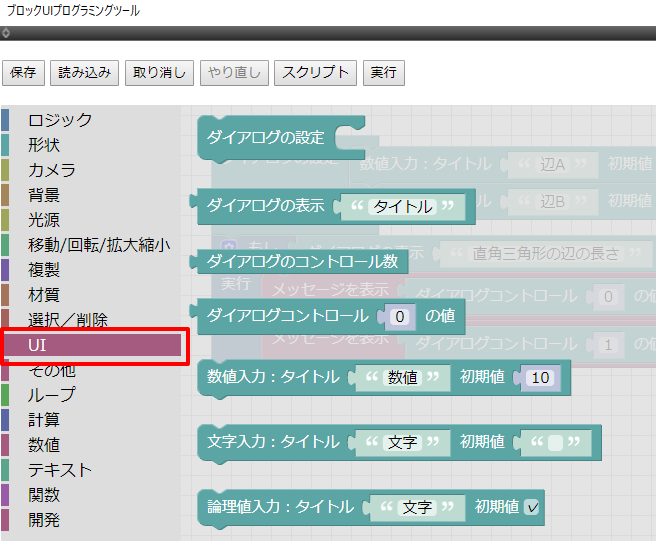
「ダイアログの設定」を配置。
「数値入力」を2つ配置して縦に連結します。それぞれに対して、タイトルと初期値を入力します。
これを「ダイアログの設定」の中につなげました。

これで、ダイアログボックスのUIとしての設定は完了です。
まだこれだけではダイアログボックスは表示されません。
「ダイアログの表示」ブロックを配置することでダイアログボックスが表示されます。
このブロックは、表示されたダイアログボックスで「OK」ボタンを押すと1、「キャンセル」ボタンを押すと0が返されます。
この「戻り値」(return)を使って、ツールボックスの「ロジック」より「もし」を配置して組み合わせます。
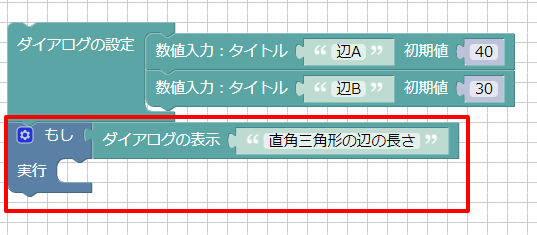
ツールボックスの「UI」で「ダイアログコントロールの値」ブロックを使用することで、指定番目の入力値を得ることができます。

ここで指定する番号は、0から始まる整数を指定します。
「ダイアログの設定」で指定した、数値や文字ブロックを順番に数えたときの番号(0, 1, 2, 3,,,)を指定することになります。
入力値を使って直角三角形を表示
次にダイアログボックスで入力された辺Aと辺Bの数値を変数に代入します。
ツールボックスの「数値」で変数AとBを作成して、ダイアログコントロールの値を入れました。

ツールボックスの「形状」で「点の位置を指定して線を作成」ブロックを配置し、
その中に「点の位置」ブロックを3つ配置しました。
また、「線を閉じる」のチェックボックスをオンにしています。
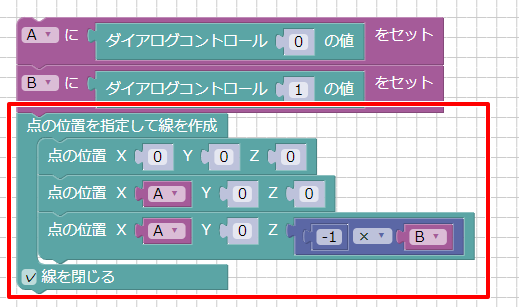
三角形はShade3Dの図形ウィンドウの上面図で見たときに直角三角形となるようにするため、XZに値を入れていきます。
ツールボックスの「数値」より変数「A」「B」のブロックを追加して以下のように3つの点に値を指定しました。
(0, 0, 0)
(A, 0, 0)
(A, 0, -B)
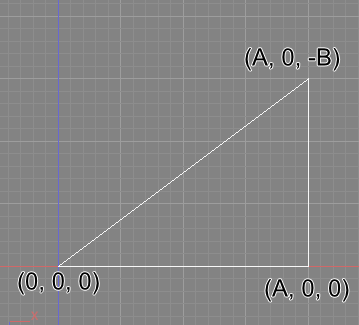
最後だけ「-B」となるように、「-1 x B」の値を入れるようにしています。
これは、Shade3DではZ軸方向が上面図では下方向がプラスになるための変換です。
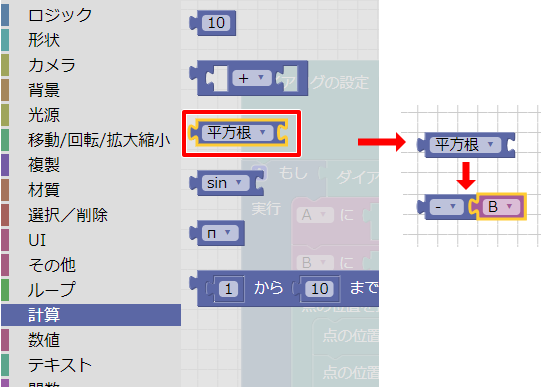
なお、ツールボックスの「計算」から「平方根」ブロックを配置し、
「-」に選択を変えてから変数Bを連結することでも、数値をマイナス値にすることができます。
この直角三角形を表示するブロックを、「もし」の結果として連結して以下のようにしました。
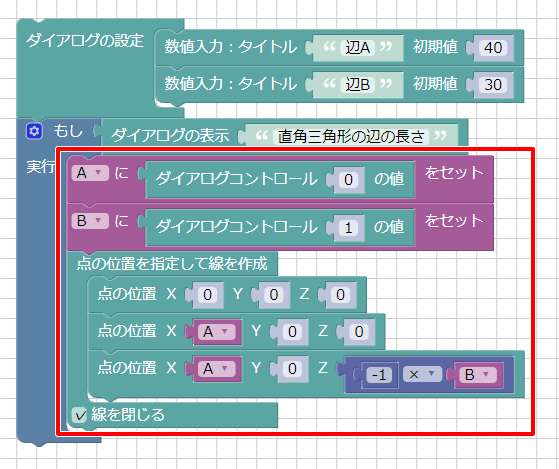
実行するとダイアログボックスが表示され、入力値の辺の長さにより直角三角形が配置されました。
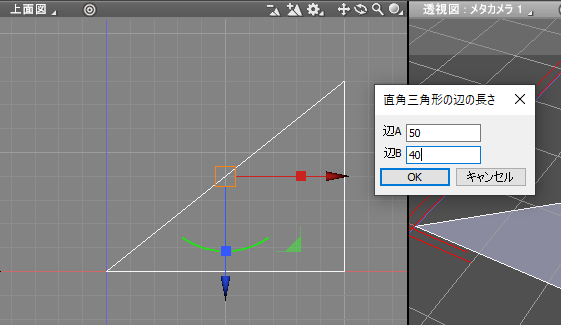
斜辺の長さを計算
ここでは、直角三角形の辺Aと辺Bの長さを変数Aと変数Bに格納しています。
これらを使用して直角三角形の斜辺の長さを計算する式は以下のようになります。
C = √(A2 + B2)ブロックUIプログラミングツールでの二乗の計算は、計算のブロックで「^」を指定することで行えます。
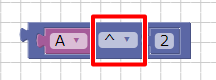
ツールボックスの「計算」で「平方根」のブロックを選択して、以下のように組み合わせました。

このブロックで返される結果が直角三角形の斜辺の長さになります。
算数/数学での演算記号をコンピュータで扱う
算数や数学で使われる演算の記号と、コンピュータ上で使われる記号について整理しておきます。
プログラムは、キーボードで入力できる文字を使って書くことになります。
キーボードを眺めても「÷」や「A2(二乗の表現)」「≧」などは存在しないのを確認できます。
「x」はありますが、これは英字の「エックス(X)」です。
プログラム(プログラミング言語)は英語圏の表記になり、「ASCIIコード」というもので制御文を記載することになります。
ASCIIコードはキーボードで見えているAからZのアルファベットや数値、記号、Enterやスペースなどを指します。
ひらがな表記は日本語特有のもので、ASCIIコードには含まれません。
「÷」「A2」「≧」などもASCIIコードには含まれません。
これらの演算の記号は以下のように置き換えて使います。
※ ここでは「プログラム」ではなくあえて「コンピュータ」と書いています。
よく使われるのがこの記載というだけで、プログラムでこの演算記号を使うというわけではありません。
| 算数/数学 | コンピュータ |
|---|---|
| + | + |
| – | – |
| × | * |
| ÷ | / |
| A2 | A^2 |
| ≧ | >= |
| ≦ | <= |
プログラミングにおいて、四則演算の場合は上記の記号を使います。
累乗の場合は、Python言語の場合は「A ** 2」と書き、C/C++言語の場合はstd::pow(A, 2.0)のように記載します。
BASIC言語の場合は「A ^ 2」と書きます。
プログラミング言語によって、計算の書き方が異なります。
平方根は「関数」として「sqrt」が使われますが、これもプログラミング言語によって書き方が異なります。
これらの演算記号は「算数/数学」の場合、「コンピュータ」としての(よく使われる)記載、「プログラミング」としての記載、でそれぞれ異なるということを頭に入れておいてください。
斜辺の長さを計算して、メッセージウィンドウに表示
変数Aと変数Bより、直角三角形の斜辺の長さを計算してメッセージウィンドウに表示するブロックは最終的には以下のようになりました。
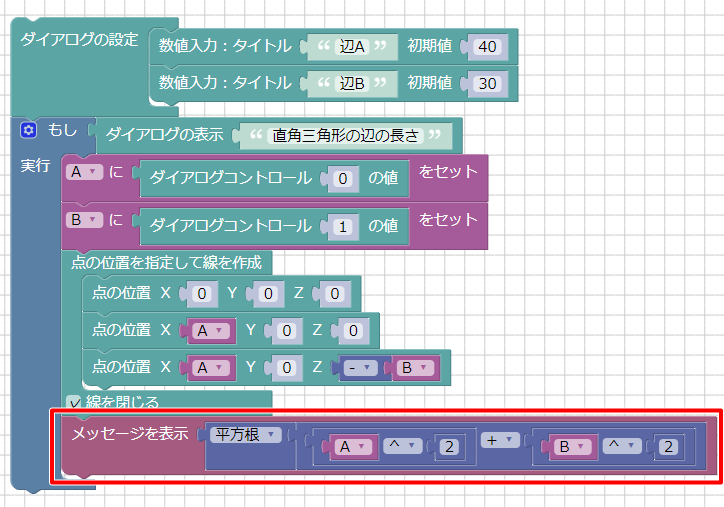
これを実行すると、辺Aと辺Bの長さを入力するダイアログボックスが表示され、指定の長さで直角三角形が描かれます。
また、メッセージウィンドウに斜辺の長さが表示されます。
関数の使用
上記のブロックは画面に収まる範囲になっていますが、さらに入力する項目が増えたり計算が複雑になるとどうなるでしょうか。
目では追いかけにくくなります。
プログラミングでは機能ごとに分離して管理するため「関数」を使用することができます。
プログラミング言語によっては「サブルーチン」と呼ばれます。
数学でも「関数」は使われます。
直角三角形の辺Aと辺Bが直角の場合に斜辺の長さを求める「C = √(A2 + B2)」も関数と呼びます。
大雑把に表現すると「入力があり、何かしらの処理を行って結果を出力するもの」が関数になります。
ブロックUIプログラミングツールでも関数を使用することができます。
簡単な関数の使用例
例として変数Aと変数Bの足し算を行い、結果を返すだけの関数を説明します。
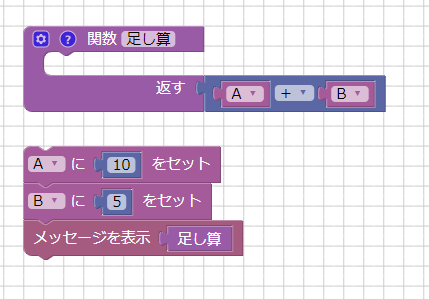
この処理の流れを図で表すと以下のようになります。
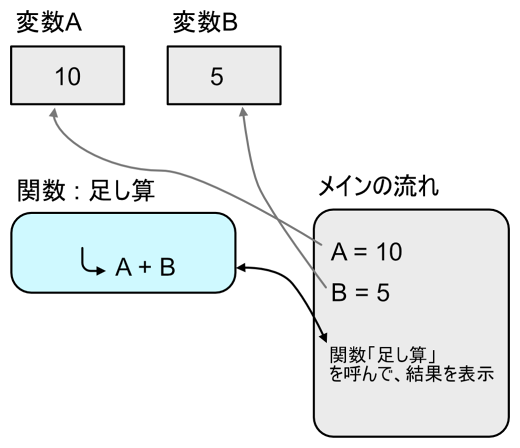
このブロックを構成していきます。
ツールボックスで「関数」を選択すると、関数として値を返さないものと値を返すものがあります。
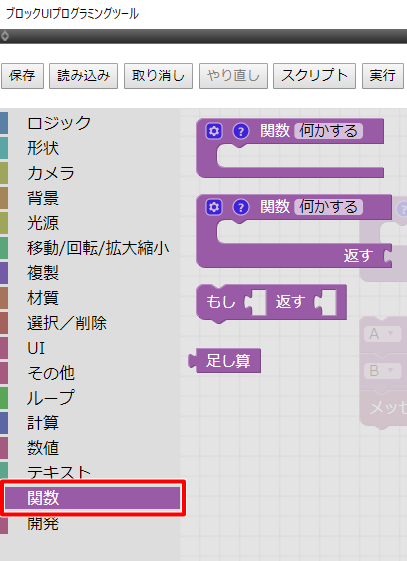
ここでは足し算を行う関数として使用するため、は結果を返すブロックを選択します。
関数では「関数名」を必ず指定する必要があります。
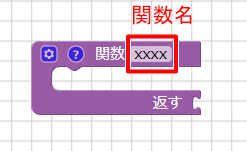
ここでは「足し算」という名前を指定しました。
複数の関数を使用する場合、関数名は同一の名前を指定できません。
この関数ブロックの「返す」のところに「A+B」を連結させています。
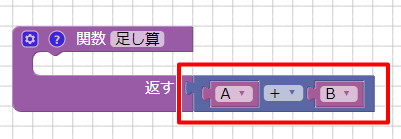
関数名を指定すると、ツールボックスの「関数」で指定された関数名のブロックが新たに追加されています。
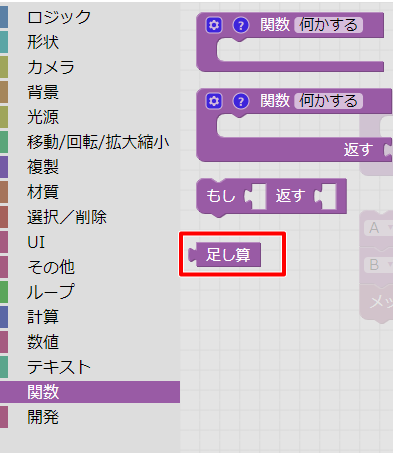
これを使用することで、対象の関数を呼ぶことになります。
その結果をメッセージウィンドウに表示する、という流れになります。
直角三角形の斜辺の長さを計算する処理を関数で分ける
直角三角形の斜辺の長さを計算するプログラムに戻ります。
まず、直角三角形の斜辺の長さを計算するブロックの流れを機能別に分けます。
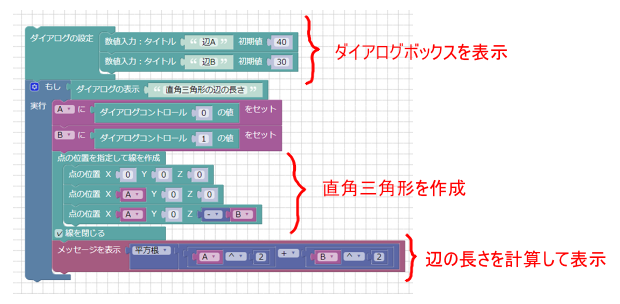
変数Aと変数Bを受け皿にして大きく3つの処理に分かれています。
ダイアログボックスの処理と直角三角形の作成を関数化していきます。
「ダイアログの表示」という戻り値のある関数を作成しました。
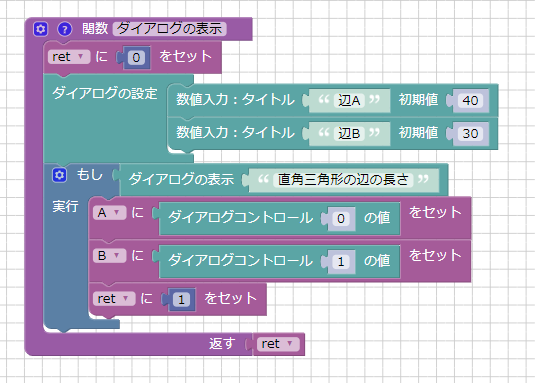
関数内で変数retを追加し初期値0を入れておきます。
これは、ダイアログボックスでOKボタンを押して確定されたときに1を入れます。
関数の戻り値としてこのretを返しています。
この関数は、ダイアログボックスを表示して変数Aと変数Bに入力値を入れる処理を行っています。
「直角三角形の作成」という戻り値のない関数を作成しました。
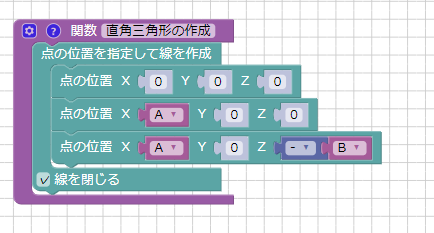
これは、変数Aと変数Bを使って上面図で見た直角三角形を作成しています。
次にメイン処理部のブロックを配置します。
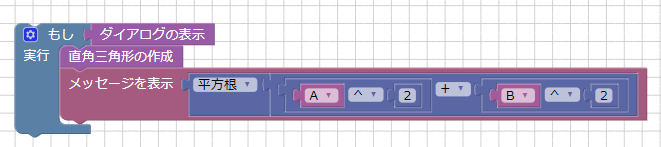
ずいぶんシンプルになりました。
関数「ダイアログの表示」を呼び、戻り値が1の場合(ダイアログボックスでOKボタンが押された場合)、
関数「直角三角形の作成」を呼んで、直角三角形を作成しています。
そして、変数Aと変数Bより直角三角形の斜辺の長さを計算してメッセージウィンドウに表示しています。
以上をすべて表示すると以下のようになりました。
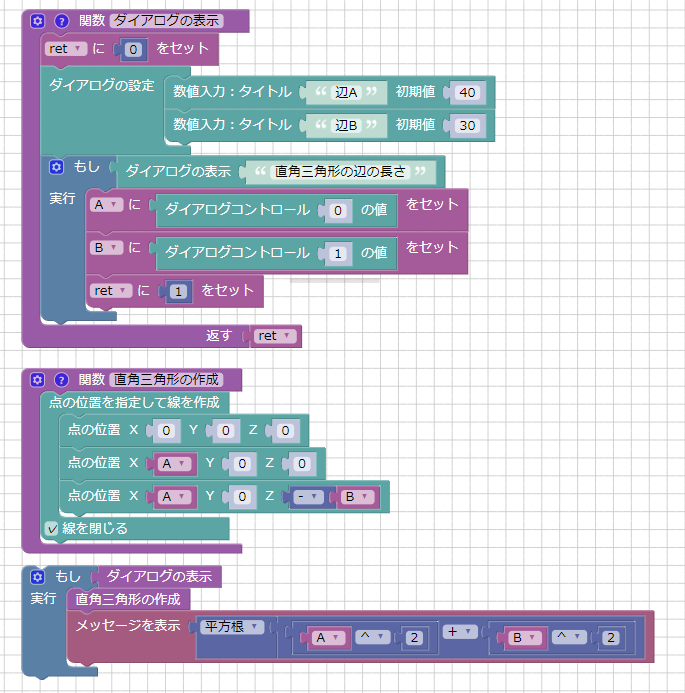
関数化したことで、それぞれの処理が見やすくなりました。
今回はここまでです。
どの部分を関数化すればいいかというのは処理を機能別に分けていくことになり、
これ自身が流れをよく理解しているか、という論理的な思考が試される部分となります。
プログラミングではただ単に処理を記述するだけではなく「分かりやすくする」(読みやすくする、可読性とも言います)のも大事な要素です。
このあたりが見えてくれば、プログラミングとして一気に視界が広がっていくと思われます。
次回はさらに踏み込んだ解説していく予定です。