![]()
- 体積
- 小数点の精度について
- 面積や体積の単位変換
- 変数とループ
Shade3D Professional版では体積の計算を行う機能があります。
今回は、ブロックUIプログラミングツールで作成した立体の体積を確認していきます。
その後、プログラミングで使う変数やループについて説明していきます。
今回の最終課題は、ピラミッドをブロックUIプログラミングツールで作成します。
立体の体積
「体積」は、立体全体の中身も含めた大きさ/容量のことを指します。
四角形や円など平面上の形状の場合は、面積は存在しますが体積は存在しません。

球や直方体などの立体は体積が存在します。

直方体の体積
直方体の底面が100 x 100(mm)、高さが50(mm)の場合、体積は100 x 100 x 50 = 500000と計算できます。
底面の面積に対して高さをかけることで体積が求まります。
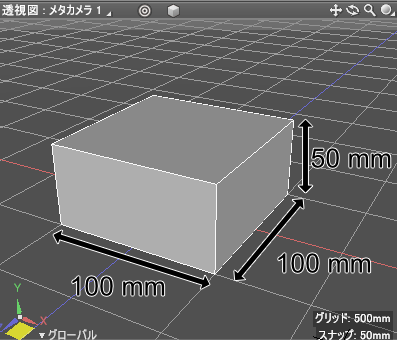
この時の単位は「mm3」(立方ミリメートル)と書きます。
[問題 1] 上記の底面が100 x 100(mm)、高さが50(mm)の直方体の単位をセンチメートルとしたときの体積を計算しましょう。
単位も出すようにしてください。
[答え 1] 500 cm3 (立方センチメートル)
直方体の底面をセンチメートルに変換すると、10 x 10(cm)、高さが5(cm)になります。
これらをより「10 x 10 x 5 = 500」と計算できます。
球の体積
半径Rの球の体積は公式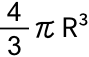 で計算できます。
で計算できます。
πを3.14としたとき、半径50(mm)の球の体積は「4 ÷ 3 x 3.14 x 50 x 50 x 50 = 523333.3333 mm3」となります。
これをブロックUIプログラミングツールとShade3Dの機能で計算してみましょう。
ブロックUIプログラミングツールのツールボックスで「作成」の「球体の作成」を選択します。
半径を50として「実行」ボタンを押します。
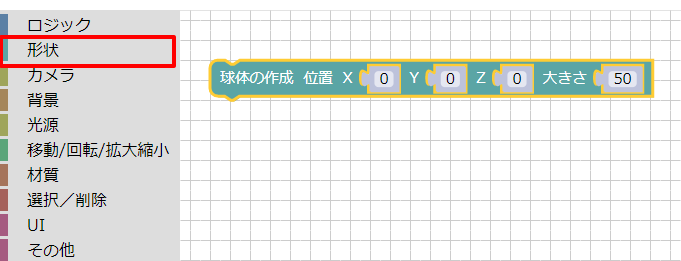
これで、半径50(mm)の球が生成されました。
コントロールバーの「測定」で「体積」を選択します。
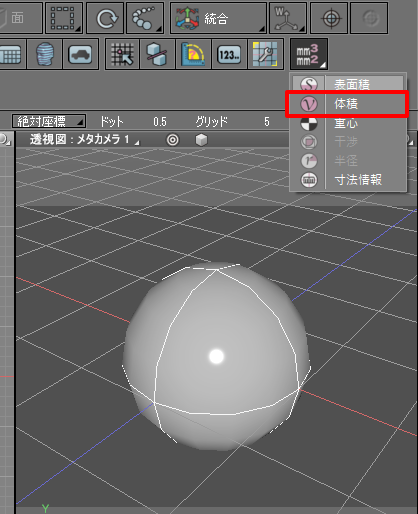
なお、この測定機能はShade3D Professional ver.18以降で使用できます。
測定情報ウィンドウが表示され、「体積(mm3)」のところで「523598.7756」と表示されました。
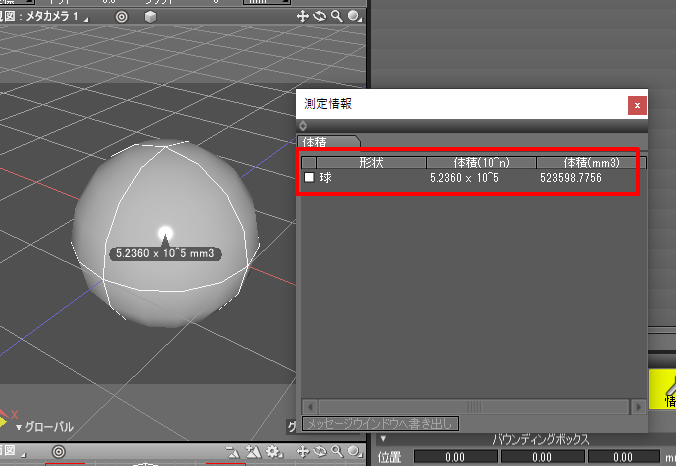
※ 「mm3」は「mm3」と同じ意味です。
先ほど計算した「523333.3333 mm3」と異なります。
この違いは、円周率(π)の値をより正確に入れているかという差で起きます。
「算数」では円周率は「3.14」で扱いますが、実際は「3.1415926535…」と割り切れない小数が続きます。
では、改めてこのより細かい円周率を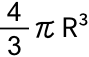 の公式に当てはめて計算します。
の公式に当てはめて計算します。
「4 ÷ 3 x 3.1415926535 x 50 x 50 x 50 = 523598.7755833… mm3」となりました。
これで、Shade3Dの測定機能の体積で表示された「523598.7756」に近づきました。
小数点の精度について
少し脱線し、コンピュータの中の話を書いておきます。
円周率のように「割り切れない数」がある場合、小数点以下何ケタかで打ち切るというのを行います。
例えば円周率は「3.1415926535…」と続きます。
算数では「小数点以下2ケタで四捨五入」を行い「3.14」を採用しています。
3DCGや設計用のCADでは、円周率を「3.14」として計算することはまずありません。
3.14のままだと精度が十分でないためです。
この「精度」は数値を表現する有効ケタ数はいくつか、というのに左右されます。
実際は10進数としてではなく、2進数としてのケタ数が影響します。
前回チュートリアルに書いたようにコンピュータ内部は2進数で扱われており、
小数点以下何ケタまで扱えるかというのに制限が入ります(プログラムとして、数値演算に特化して有効ケタ数を増やすことは可能です)。
では、その有効ケタ数を超えた計算が行われるとどうなるでしょうか?
その場合は小数点以下の値が小さくなるほど「誤差」が含まれることになります。
大雑把な書き方をすると「誤差」は、より正確な値と比較して正しくない値になっている差分を指します。
3DCGのツールであるShade3Dはある程度の精度は確保しますが、微生物サイズ(1000分の1ミリメートル以下)になると誤差を考える必要があります。
0.001(mm)だと問題ないのではと思われるかもしれませんが、この体積を計算するとなると3乗なので 0.001 x 0.001 x 0.001 = 0.000000001となり、
かけ算/累乗が発生することであっという間に小さい値になっていきます。
「累乗」とは、10のn乗 (10nと記載します)のように表現する場合は、10をn回かけ算する計算です。
Shade3Dでは、内部で64ビット(2の64乗)で小数値を表現します。
計算時は32ビット(2の32乗)で扱う部分もあります。
これらにより有効ケタ数が決められ、精度もそれに左右されることになります。
算数や(中学校の)数学の範囲の場合は、精度の限界はさほど気にしなくても問題なさそうですが、
割り切れない数が答えとして出てくる場合もありますので、
「小数点何ケタで四捨五入、もしくは切り捨て」という条件が出てくることもあります。
難しい話にはなりますが、コンピュータは無制限に正確というわけではない、というのを頭に入れておきましょう。
円柱の体積
円柱の体積は、底面の円の面積に高さをかけた計算で求めることができます。
底面の円の半径がRのときの円柱の体積は「円柱の体積 = π x R2 x 高さ」になります。
これをブロックUIプログラミングツールとShade3Dの機能で確認してみましょう。
[問題 2] 半径50(mm)、高さ100(mm)の円柱をブロックUIプログラミングツールで作成し、体積を計算しましょう。
πは3.14、体積の単位は「cm3」とします。
[答え 2] 785 cm3
半径50(mm)、高さ100(mm)の単位をcmに変換します。
半径5(cm)、高さ10(cm)となります。
公式に当てはめて計算すると、「π x R2 x 高さ = 3.14 x 5 x 5 x 10 = 785」となります。
ブロックUIプログラミングツールで円柱を配置して体積を計算します。
ブロックUIプログラミングツールのツールボックスの「作成」で「円柱の作成」を選択。
半径を50、高さを100とします。

「実行」ボタンを押すと円柱が配置されます。
コントロールバーの「測定」で「体積」を選択します。
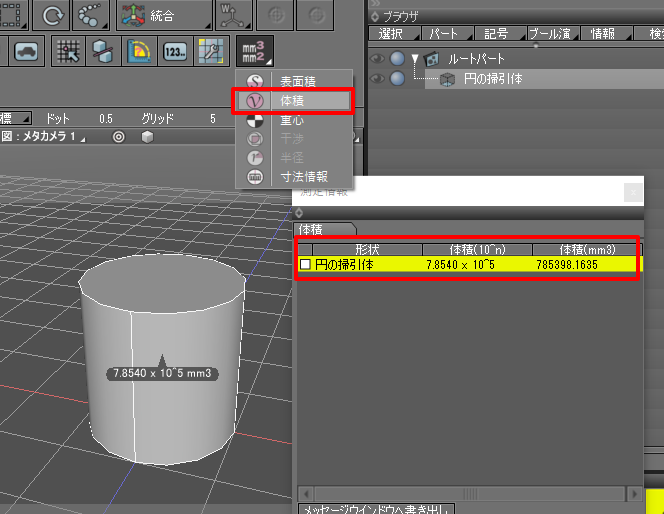
測定情報ウィンドウで「体積(mm^3)」は「785398.1635」となりました。
これは「mm3」なので単位変換します。
mmからcmの変換は0.1倍。
mm3からcm3の変換は3乗になるため、0.1の3乗=0.001倍。
「785.3981635 cm3」になります。
小数点以下を切り捨てると「785」となり、公式に当てはめて計算した結果と同じ値になりました。
面積や体積の単位変換
今まで面積や体積の単位を変換する場合は、計算前の距離値を先に単位変換していました。
再度「単位」の意味を把握し、そこから面積や体積の単位を相互変換していきます。
距離の単位は「mm」(ミリメートル)や「cm」(センチメートル)。
面積の単位は「mm2」(平方ミリメートル)や「cm2」(平方センチメートル)。
体積の単位は「mm3」(立方ミリメートル)や「cm3」(立方センチメートル)。
「2」は累乗の指定となり、同じ値を2回かけ算する指定です。
「3」は、同じ値を3回かけ算する指定です。
距離の単位として「mm」から「cm」に変換する場合は、0.1倍することになります。
「mm2」から「cm2」に変換する場合は、2乗があるため「0.1 x 0.1 = 0.01」倍することで面積の単位を変換できます。
「mm3」から「cm3」に変換する場合は、3乗があるため「0.1 x 0.1 x 0.1 = 0.001」倍することで体積の単位を変換できます。
また直方体や円柱などの場合、体積を高さで割ると底面の面積が求まることになります。
この時の単位を見ると、体積 ÷ 高さ = mm3 ÷ mm = mm x mm x mm ÷ mm == mm x mm = mm2、という計算になります。
このように単位があることで、それぞれの相互変換に役立ちます。
変数
プログラミングでも使われる「変数」について書いていきます。
いよいよプログラムに近づいていくことになります。
ここで出てくる単語は算数の用語ではなく、プログラミング用語になります。
底面の円の半径がRの円柱の体積は「円柱の体積 = π x R2 x 高さ」となります。
ここでの「π」は円周率になり、算数では「3.14」を使用します。
この値は変化しませんが、精度を上げるために「3.1415926535」と小数点のケタ数を増やして表現する場合もあります。
このときのπは「定数」と呼ばれます。
定数は固定の値になり、変化しません。
一方「変数」は、円柱の底面の半径「R」のように値が変化するものを入れる「入れ物」になります。
以下は円柱の底面の円の半径をR、高さをHとしたときに、R=50、H=100を入れた場合の図です。
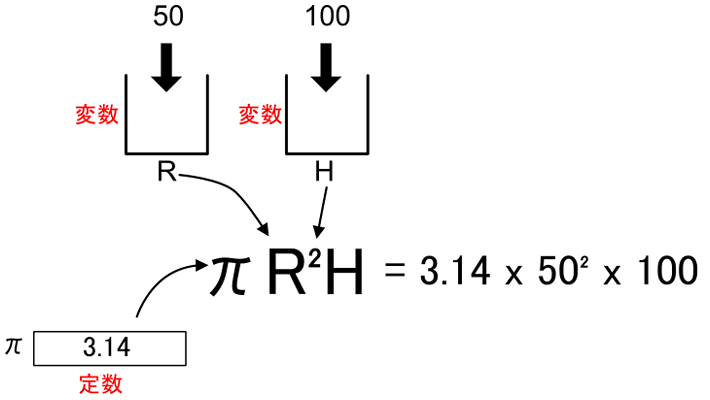
この場合はRとHが変数に相当します。
ここでは単純に変数に数値を入れているだけですが、整理して段階的に計算を進めていく場合にも使用します。
では、次に変数を使わないと手間がかかる場合を考えていきます。
ブロックUIプログラミングツールの「変数」
ブロックUIプログラミングツールで「変数」のブロックを作成します。
ツールボックスの「数値」で「数の変数を作る」を選択し、新しい変数の名前を入力します。
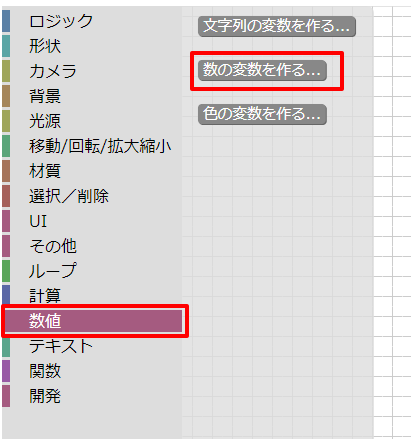
変数名を「A」としました。
メニューから「Aにセット」と「A」を選択できるようになります。
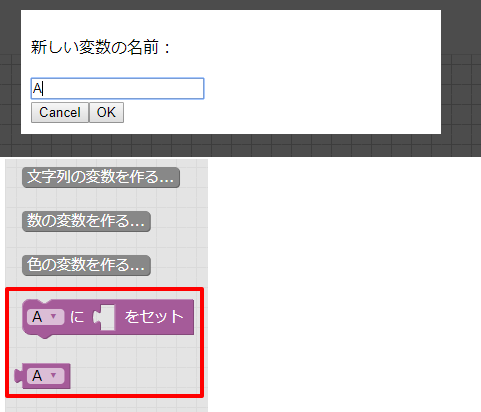
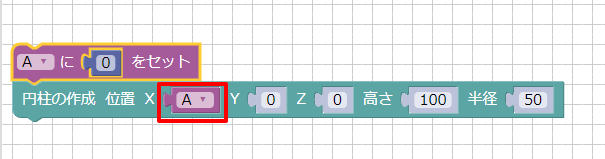
Aに対して値を指定する場合は「Aにセット」のブロックを使います。
以下の場合は、Aに0を指定しています。
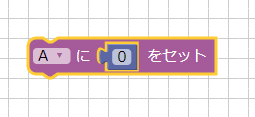
数値のブロックは、ツールボックスの「計算」から選択できます。
Aの値を使う場合は、ツールボックスの「数値」から「A」のブロックを配置します。
以下は、円柱の位置XでAの値を使用しています。
ブロックUIプログラミングツールの「ループ」
「ループ(繰り返し)」は、ある処理を指定回数繰り返す仕組みです。
ツールボックスの「ループ」より「10回繰り返す」ブロックを選択します。
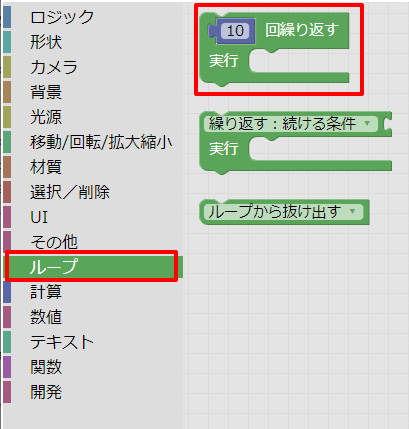
これは、この中に指定した処理を10回繰り返して行う機能です。
この「繰り返し」をプログラミングでは「ループ」と呼びます。
次に、実例として「変数」と「ループ」を組み合わせた立体の作成を行います。
ブロックUIプログラミングツールで複数の形状を並べる
[問題 2] 底面の円の半径50(mm)、高さ200(mm)の円柱を配置します。
このとき、円柱の底面の中心を原点とし、X軸方向に150(mm)間隔で合計10個並べる処理をブロックUIプログラミングツールで作成しましょう。

[答え 2] 以下のようにブロックを配置しました。
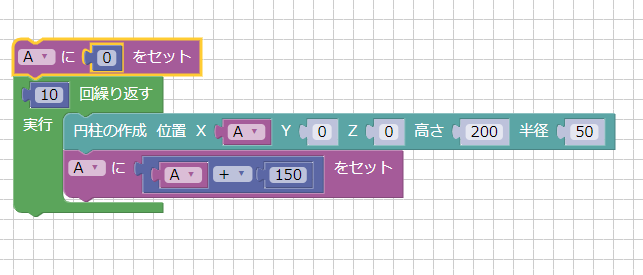
変数として「A」を作成し、0を入れておきます。
円柱をX軸方向に150(mm)間隔で配置する際に使用します。
ループの「10回繰り返す」ブロックを配置し、その中に「円柱の作成」を配置します。
位置Xは変数Aを使用し、YとZは0、高さを200、半径を50としました。
変数Aの値をX値として使用し、円柱を配置することになります。
Aに対して「A+150」を入れています。これにより、変数Aはループごとに0,150,300,450,600と増加します。
これを実行すると、原点位置からX軸方向に150ずつ離れて円柱が配置されることになります。
この流れを図として書くと以下のようになります。
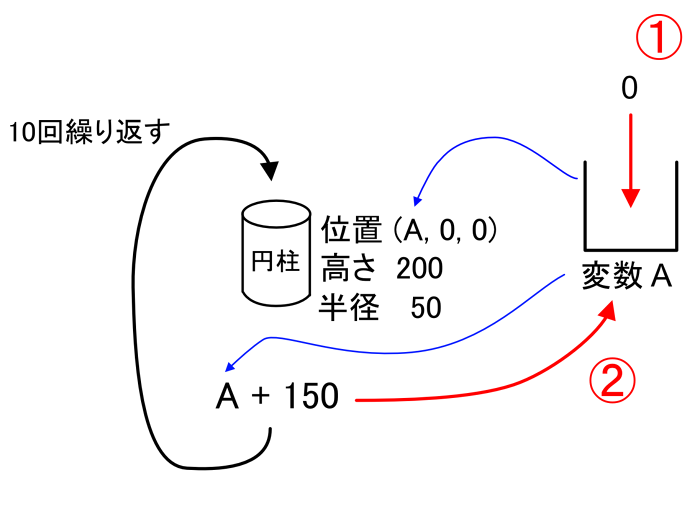
変数Aは入れ物となり、はじめに0を入れます。
ループを繰り返すときに円柱の位置XでAを使用して円柱を作成。
その後、AにA+150を入れます。
プログラム的に書くと「A = A + 150」を行います。
これを10回繰り返すことで、円柱の底面の中心のX値は0,150,300,450,600,750,900,1050,1200,1350と変化します。
Aは値を使用する場合もセットする場合も、同じ「入れ物」を使いまわすことになります。
これで「指定の円柱を等しい間隔で複数並べる」が実現できました。
これが「プログラム」になります。
もっと複雑なプログラムはコンピュータ言語を記載することになりますが、
この処理の「流れ」についてはすべてのプログラミングにおいて共通です。
「プログラム」とはこのような流れ自体を指します。命令の組み合わせになります。
「プログラミング」はそのような流れを組む作業のことを指します。
この「ループ」のような特定の動きを行う仕組み/組み立てを「構文」と呼びます。
ループの場合は繰り返し回数や繰り返し条件を指定する必要があります。
構文は、このループのように何かしらルールがあります。
「ループ」以外に、条件によって分岐する処理も構文としてよく使われます。
これらを組み合わせたプログラムについては、次回解説していく予定です。
プログラミングは、まず先に変数と構文を理解していくのが習得の第一歩になります。
このときの論理的な考え方は、算数や数学に非常に似ています。
ピラミッドを作る
今までは算数として計算を中心に説明していましたが、絵を作る場合にプログラミングがどのように使えるか確認していきます。
ここでは段差のあるピラミッドを作成します。
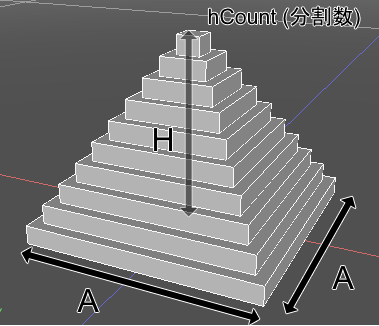
変数として以下を用意しました。
これは「入力用」の変数となり、この値は事前に与えます。
- A : 底面の正方形の一辺の距離
- H : ピラミッドの高さ
- hCount : ピラミッドの高さ方向の分割数
入力と出力
プログラミングでは、何か値を与える操作は「入力」(英語ではインプット(Input/In))と呼ばれます。
結果として作られるものは「出力」(英語ではアウトプット(Output/Out))と呼ばれます。
入力/出力の対象は数値や文字列/画像/3D形状など、さまざまです。
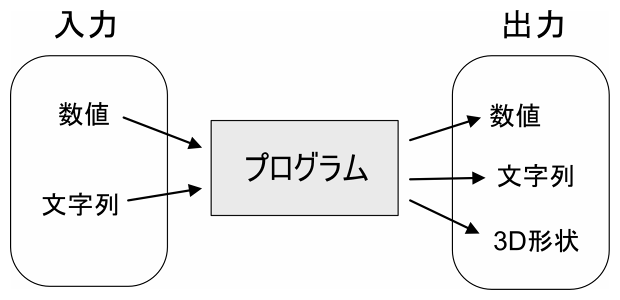
なお、数値や文字列などの単体では意味をなさないものを「データ」と呼びます。
データが合わさって整理されて意味を持ったものは「情報」と呼ばれます。
プログラムは、入力値を元に計算や加工を行い、結果を出力として出す仕組みといえます。
ブロックUIプログラミングツールでピラミッドを作る
ブロックUIプログラミングツールでピラミッドを作成します。
入力情報として、「A」「H」「hCount」を変数として作成します。
(ツールボックスの「数値」から変数を作成します)
「値」はツールボックスの「計算」からブロックを配置します。
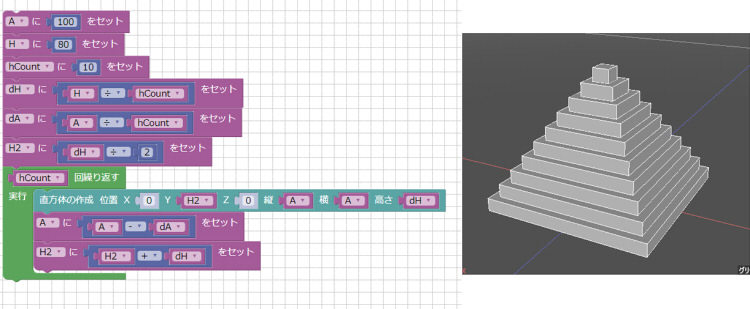
以下のように、Aの値を100、Hの値を80、hCountの値を10としました。
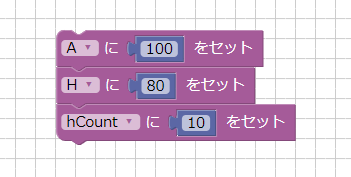
直方体を原点位置を中心に上に積み上げていくプログラムを書くことになります。
その時にループを使い、ループの繰り返し回数はhCountの変数の値を使います。
はじめの直方体のサイズは、位置(0, (H ÷ hCount) ÷ 2, 0)、底面のサイズはA、高さは(H ÷ hCount)となります。
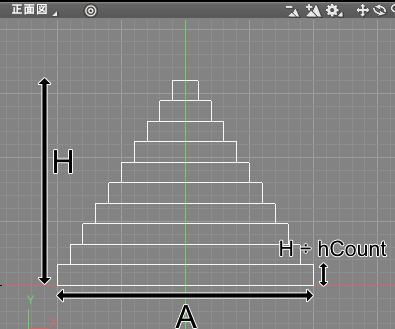
直方体の中心位置のYを「直方体の高さ ÷ 2」とすることで、直方体の底面を原点位置にしています。
また、高さ(H ÷ hCount)は直方体を上に積み上げていっても変化しません。
この直方体の高さは変数dHに格納しました。
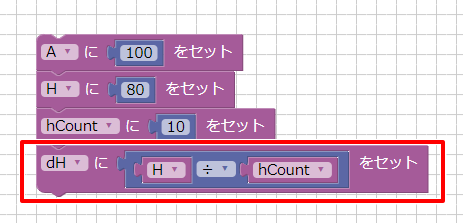
直方体は積み上げていくごとに底面のサイズが小さくなっていきます。
一辺のサイズAの左右から「A ÷ hCount ÷ 2」を引く計算になります。
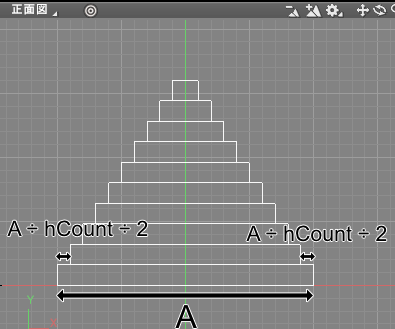
両端を短くするため、「A ÷ hCount ÷ 2 x 2 = A ÷ hCount」をループの繰り返しごとにAから引いていくことになります。
変数dAを追加し、「dA = A ÷ hCount」としました。
また、直方体の初期位置Yは「dH ÷ 2」となります。これを変数H2に格納しました。
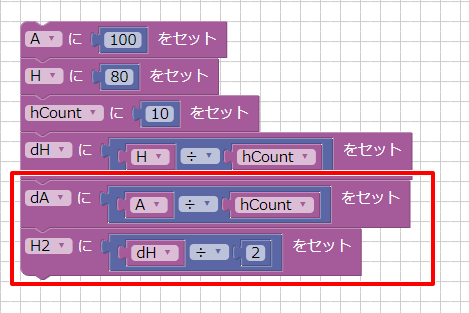
次にループを配置します。
ループはhCount回繰り返します。
直方体の作成は、位置(0, H2, 0)、縦と横をA、高さをdHとしています。
その後、「A = A – dA」「H2 = H2 + dH」と変数AとH2を更新します。
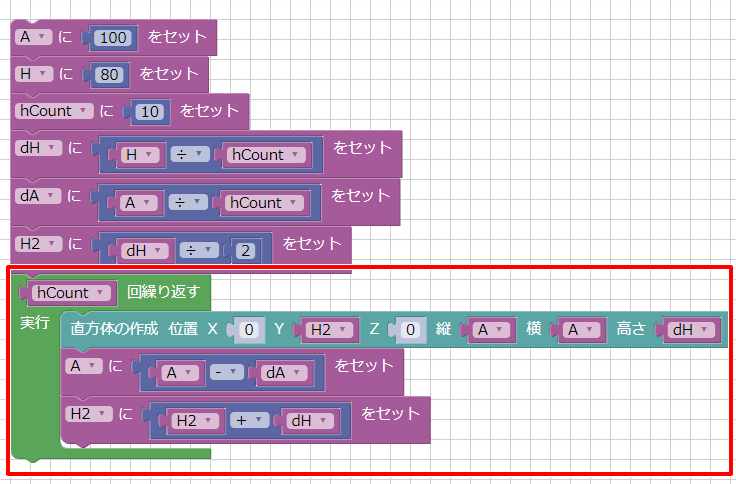
これでプログラムができました。
実行すると、ピラミッドが作成されます。
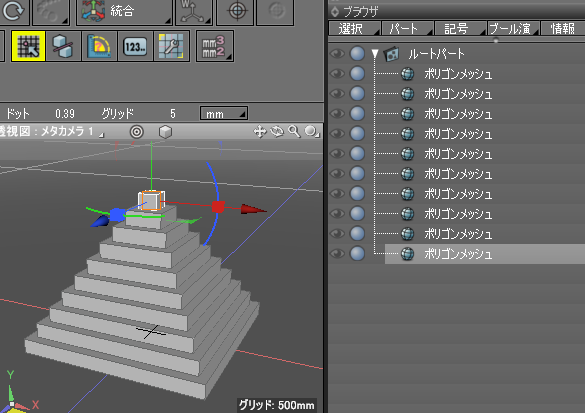
hCountの初期値を20として分割を細かくして実行すると、より細かい階段になります。
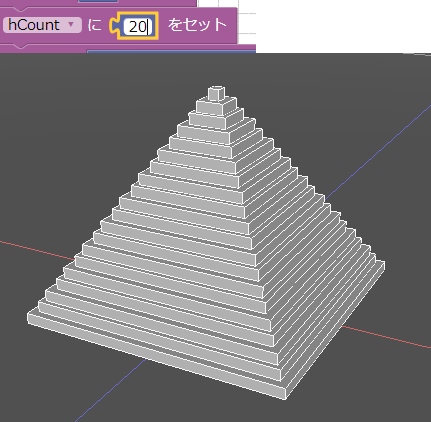
このように変数を使用すると、値を1つ変えるだけで結果を変えることができるようになります。
今回はここまでです。
算数に加えてプログラミングに触れていきました。
プログラミングは、今までの算数の基礎知識で学習した考え方を理解していないとおそらくつまづくことになると思われます。
算数とプログラミングは異なるように見えますが、算数の「解き方」や「組み立て方」は論理的になっており、
それらはプログラミングを始める前の基礎知識としても通用するものです。
次回、構文についてさらに掘り下げていきます。
算数についても、プログラミングの力を借りて理解を深めていく予定です。