![]()
- 三角関数(sin/cos/tan)
- 極座標でのsinとcosの関係
- asin/acos
上級編は中学校の知識で把握できるレベルとしていましたが、今回は高校数学の範囲である「三角関数」について書いていきます。
三角関数は3DCGでも非常によく利用されます。
論理的な理解の手助けになる関数でもあるため、ここで説明することにしました。
三角関数
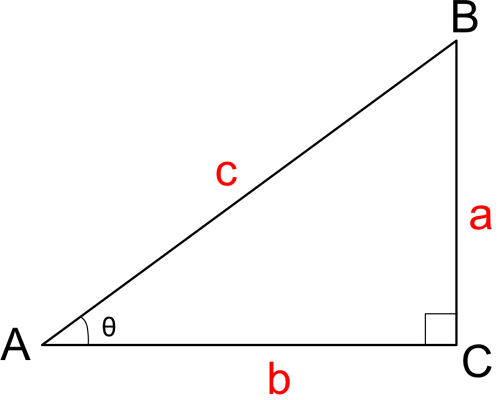
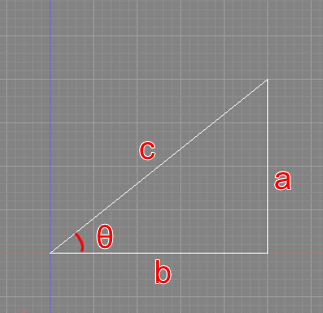
直角三角形ABCの3辺をa/b/cとします。
頂点Cの角度が直角で、頂点Aの角度をθ(シータ)とします。
このとき、以下の計算式が成り立ちます。
cosθ = b / c
sinθ = a / c
tanθ = a / b = sinθ / cosθ
このときの「cos(コサイン)」「sin(サイン)」「tan(タンジェント)」は「三角関数」と呼ばれます。
今の段階ではそういうものがあるとして、深く考えずに先に進めていきます。
後々、これらが何なのかというのを紐解いていきます。
「θ」は角度を表します。三角関数や数学での角度の指定は「ラジアン」が使用されます。
プログラミングでも、ラジアンを使用して角度指定する場合が多いです。
角度の度数指定とラジアン指定
今まで角度については「度数」で表現していました。
これは、1周を360度とする表現になります。0度=360度です。
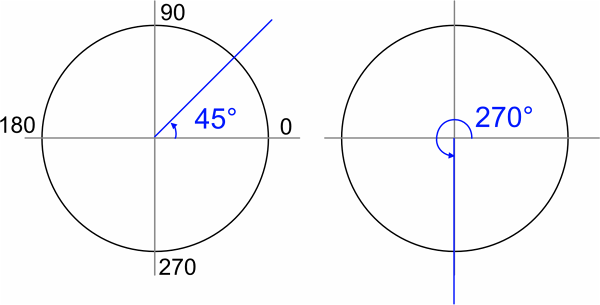
「ラジアン」で表す場合は、1周の360度が「2π」になります。
「ラジアン = (度数/360) * 2π」として置き換えできます。
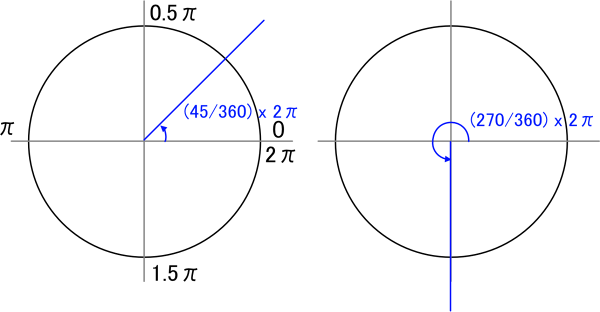
度数の式に置き換えると「度数 = (ラジアン / 2π) * 360 = (ラジアン / π) * 180」となります。
三角形の作成
直角三角形は容易に作成できるため、まずは「cos」「sin」の値を確認してみましょう。
ブロックUIプログラミングツールで三角形を作成します。
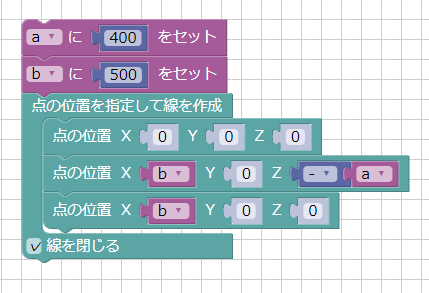
変数aとbを作成し、それぞれを三角形の辺の長さとします。
a=400、b=500としています。
ツールボックスの「形状」より「点の位置を指定して線を作成」を配置し、「線を閉じる」をオンにします。
点の位置は(0, 0, 0) (b, 0, -a) (b, 0, 0) の3点を指定しました。
これを実行すると以下のようになります。
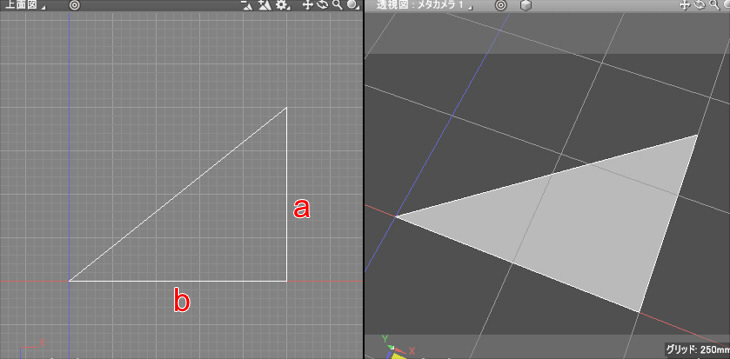
[問題 1] この三角形の斜辺の長さcをブロックUIプログラミングツールで計算しましょう。
[答え 2] c = 640.31
三平方の定理より、「c2 = a2 + b2 = √(a2 + b2)」の計算式になります。
変数cを作成して、以下のようにブロックを組み合わせました。
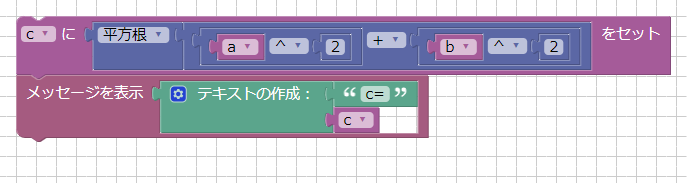
実行すると、メッセージウィンドウに「c=640.312423743」と表示されました。
斜辺cと辺bが作る角度を計算
a=400、b=500、c=640.31が判明しているとして、斜辺cと辺bが作る角度θを計算していきます。
「cosθ = b / c」を計算すると、「cosθ = 500 / 640.31 ≒ 0.7809」となりました。
「sinθ = a / c」を計算すると、「sinθ = 400 / 640.31 ≒ 0.6247」となりました。
これだけではよくわかりません。
では、そもそもcosやsinとは何なのか?ということを説明していきます。
sinとcos
原点を中心として、指定の角度θ、指定の距離rだけ離れた位置を表す座標系を「極座標」と呼びます。
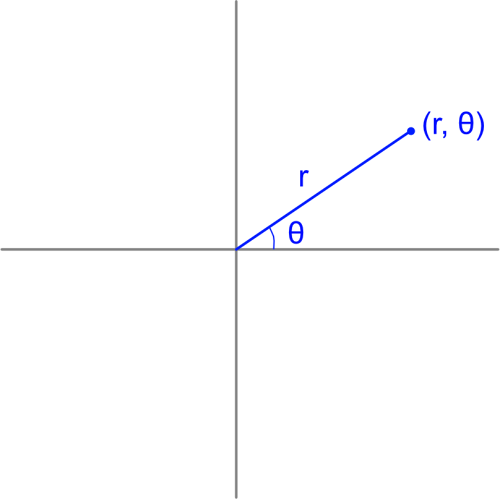
なお、従来の説明で使用していたXY軸が存在するときに(x, y)で表す座標系を「直交座標」と呼びます。
sinとcosは、半径1.0の極座標で以下のような関係になります。
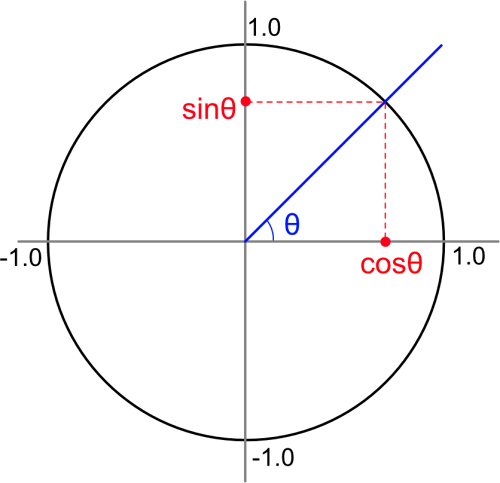
横方向をX、縦方向をYとした場合、Xは-1.0 ~ +1.0の範囲、Yは-1.0 ~ +1.0の範囲になります。
横方向がcos、縦方向がsinの値です。
三平方の定理より、「12 = (cosθ)2 + (sinθ)2」となります。
半径1の円のため直角三角形の斜辺は常に1になり、直交する2辺はcosθとsinθになります。
なお、三角関数では「(cosθ)2」は「cos2θ」と記載します。
これより「cos2θ + sin2θ = 1」が公式として導き出せます。
θは0 ~ 360度(ラジアンで0.0 ~ 2π)の角度を持ちます。
上図を見ると、cosθとsinθは-1.0 ~ +1.0となるのが分かります。
[問題 2] θが0度,90度,180度,270度のとき、cosθとsinθの値を上図を参考に求めましょう。
[答え 2] 以下のようになります。
| cos0 | 1.0 |
| cos90 | 0.0 |
| cos180 | -1.0 |
| cos270 | 0.0 |
| sin0 | 0.0 |
| sin90 | 1.0 |
| sin180 | 0.0 |
| sin270 | -1.0 |
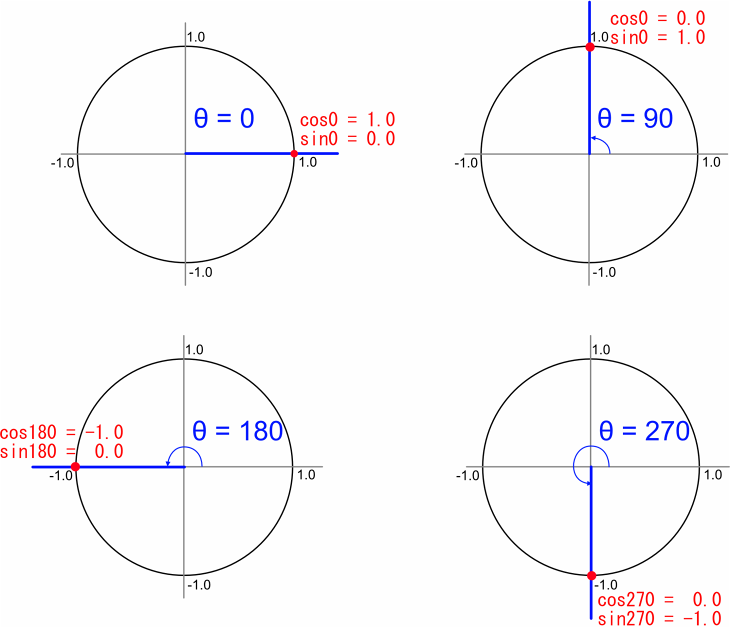
指定の角度のときのX値をcos、Y値をsinとしています。
sinとcosが分かっている場合の直角三角形の角度θを計算
では、a=400、b=500、c=640.31が判明している場合の直角三角形での角度θを改めて求めます。

「cosθ ≒ 0.7809」「sinθ ≒ 0.6247」となっていました。
「cos2θ + sin2θ」に当てはめて計算すると、
「0.78092 + 0.62472 = 1.0」となります。
これより、この極座標上の半径1.0の円の円周上に(cosθ, sinθ)が存在するのを確認できます。
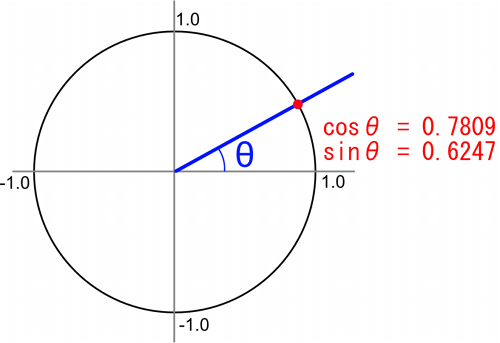
(cosθ, sinθ)を座標に当てはめて角度を分度器で測ると大雑把には角度が求まりますが、計算で求めてみます。
角度からcosθの変換を行う関数の逆の計算として「arccos(アークコサイン)」というものが存在します。
プログラミングでは「acos」とも書かれます。
同様に角度からsinθの変換の逆を計算するには「arcsin(アークサイン)」が存在します。
プログラミングでは「asin」とも書かれます。
これらの関数は、プログラミングでは標準的に使用できます。
角度θが存在する場合、「θ = acos(cosθ)」「θ = asin(sinθ)」の計算を行えます。
これは、θが0.0 ~ 90.0度(ラジアン表現で0.0 ~ π/2)までの場合の計算です。
符号を考慮すると、以下で角度をラジアンとして計算できます。
以下は、変数radに対してラジアンとしての角度を入れています。
a_s = asin(sinθ)
a_c = acos(cosθ)
もし (a_s > 0.0)の場合 rad = a_c
それ以外の場合 rad = 2π - a_c
ブロックUIプログラミングツールでの三角関数を使った角度計算
※ ブロックUIプログラミングツールでは三角関数のsin/cos/tan/acos/asinなどは、ラジアンではなく「度数での角度指定」になります。
では、ブロックUIプログラミングツールに戻り、直角三角形の角度θを計算するブロックを構築します。
以下のブロックで、辺a/b/cが求まった状態です。
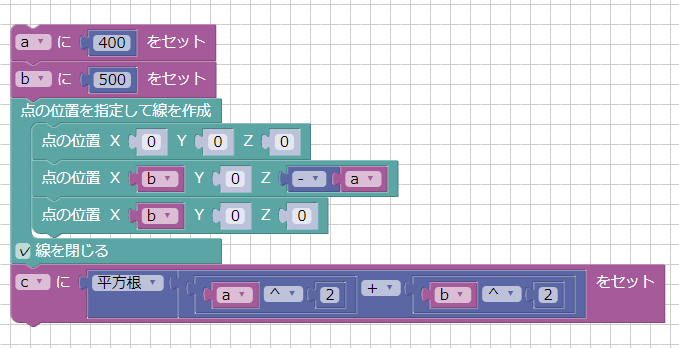
辺a/b/cから、辺bと辺cが作る角度θを計算します。
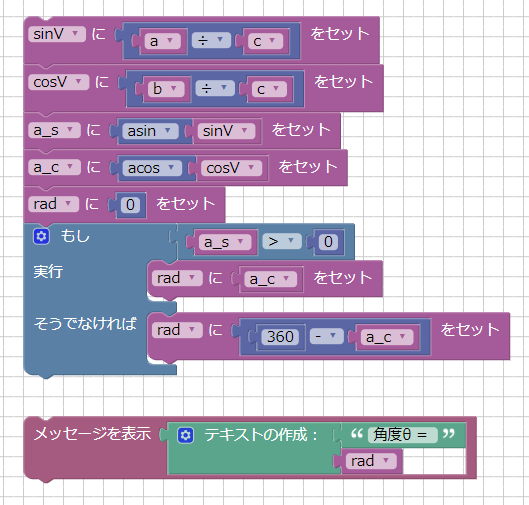
直角三角形の場合は直角を除いた角度は90度以内に収まるため「もし」の分岐は必要ありませんが、360度の角度を考慮して入れています。
「cosθ = b / c」「sinθ = a / c」の公式を使用して結果を変数「cosV」「sinV」に入れ、
「a_s = asin(sinV)」「a_c = acos(cosV)」より、度数としての角度を求めています。
三角関数は、ツールボックスの「計算」からブロックを配置できます。
なお、ブロックUIプログラミングツールでは三角関数は角度を度数として使用します。
直角三角形の角度は90度以内であるため、ここで計算されたa_sとa_cは同じ90度以内の値が入っています。
これを実行すると、メッセージウィンドウでは「角度θ = 38.6598082541」と表示されました。
これは辺bと辺cを挟む角度(度数)になります。

三角関数を使用して円周の長さと円周率を計算
三角関数を使用することで、今まで定数として扱っていたものをある程度証明していくことができるようになります。
「[中級] 符号/分数/小数/面積/円周率」で円周率について説明していました。
円周率が3.14となるのを三角関数を用いて計算してみましょう。
半径1.0の円を極座標で表します。
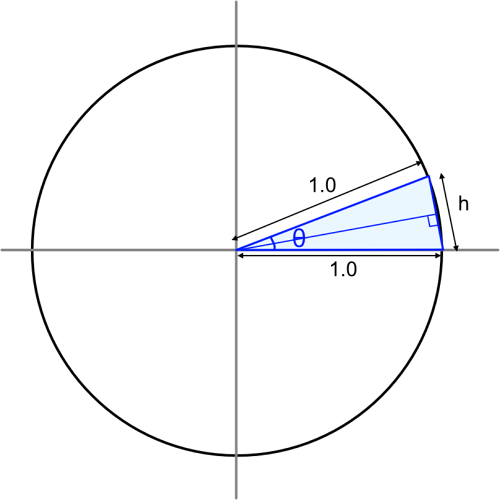
この円を角度θごとに分割します。このときの三角形は、2つの直角三角形で構成されます。
三角形の1辺をhとすると、(360 / θ) * h が円周に相当します。
角度θをより小さくすることで真円に近づきます。
三角形だけを抜き出しました。
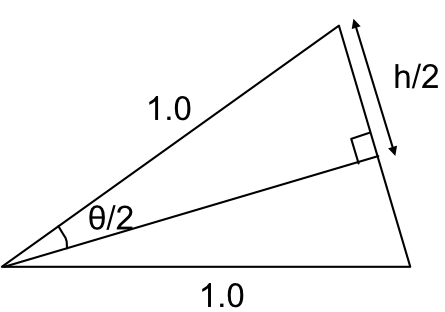
求めるのは長さhです。
半径1.0の円であるので、1辺は1.0と判明しています。
また、角度はθ/2と判明しています。
これらの情報より、三角関数の「sinθ = a / c」が使用できそうです。
sin(θ/2) = (h/2) / 1.0
h = sin(θ/2) * 2
これで長さhが求まりました。
円周の長さは、「(360 / θ) * h」より計算できます。
それでは、これらをブロックUIプログラミングツールで計算してみます。
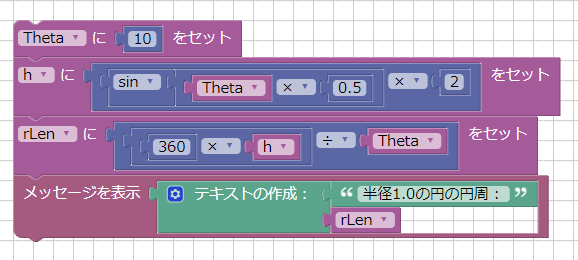
「Theta」「h」「rLen」の3つの変数を作成しました。
「Theta」は入力値として、円を分割する際の角度を度数で指定します。
この値が小さいほどより正確な円周が計算できることになります。
「h」は円を「Theta」の角度で分割した際の三角形の外側の辺の長さを入れます。
「rLen」は円周の長さを入れます。
注意点としてrLenの計算は「360 * h / Theta」と順番を入れ替えました。
これは、hが小数値のため先に整数の360とかけてからThetaで割っています。
「360 / Theta * h」とした場合は、「360/Theta」が整数値の場合に小数点以下まで求まらないため結果は正しくなくなります。
「Theta」を10とした場合、実行すると「半径1.0の円の円周 : 6.27521347783」と表示されました。
円周率は円の半径をRとしたときの「2πR」で計算できるため「rLen / 2」が円周率となります。
ブロックを以下のように追加しました。
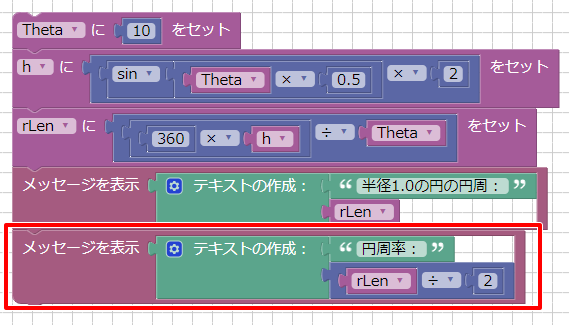
実行すると、「円周率 : 3.13760673892」と表示されました。
ここで、「Theta」の値を小さくしていった時の円周率の変化を見てみます。
| Theta(度数) | 円周率 |
|---|---|
| 10.0 | 3.13760673892 |
| 5.0 | 3.1405958903 |
| 2.0 | 3.14143315871 |
| 1.0 | 3.14155277941 |
| 0.5 | 3.14158268502 |
| 0.1 | 3.14159225485 |
| 0.01 | 3.1415926496 |
| 0.001 | 3.14159265355 |
これより、分割を細かくすることでより正しい円周率に近づいているのを確認できます。
このように公式や関数を使用することで、今までなぜこうなっていたのだろうというのが芋づる式に解けていく、という手ごたえがつかめますでしょうか。
固定の値となる部分を見つけ出して公式や関数を使って未知の値を計算していく、という処理を行う際に三角関数や数学の公式はよく使われます。
この部分は、プログラミングによる問題解決そのままの事例でもあります。
電卓でもこれらの計算を求めることができますが、
プログラムの場合は変数の値を変えるだけで手順を踏んだ計算結果を得ることができ、より作業を効率化できているのが分かるかと思います。
形状として三角関数を使用し、性質を探る
数値としての三角関数の使用はここまでにして、三角関数を使って形状を配置しsin/cosの性質を見てみます。
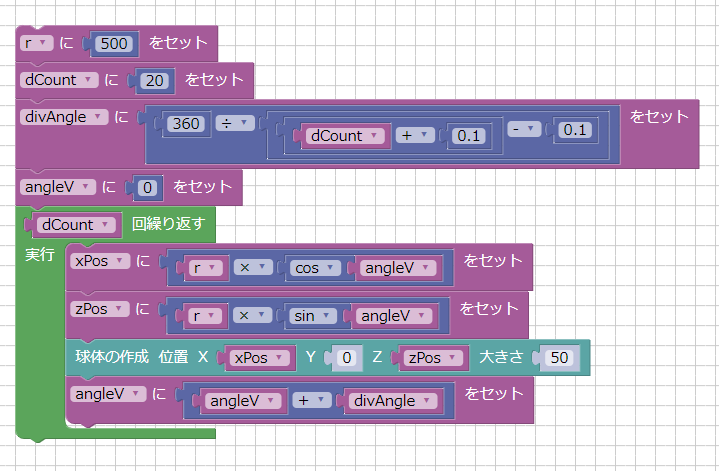
[問題 3] 半径「r」、個数を「dCount」として、半径rの円周上に半径50.0の球を配置してみましょう。
[答え 3] 以下のようにブロックを構成しました。
実行すると以下のようになります。
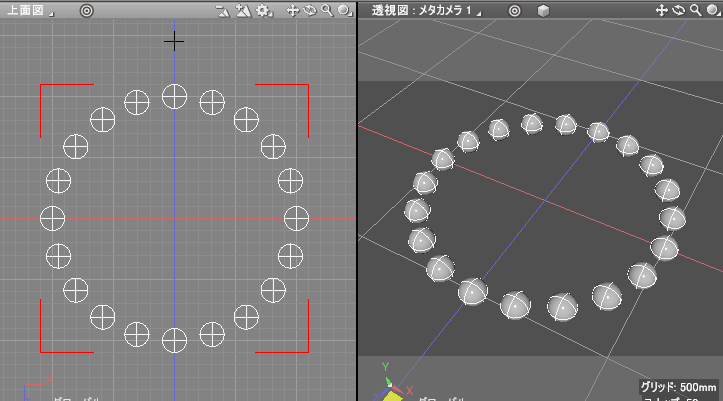
変数「r」に円の半径、変数「dCount」に配置する球の個数を整数で入れます。
ここではrを500、dCountを20としました。
変数divAngleを作成し「360 ÷ (dCount + 0.1 – 0.1)」を入れています。
0.1を足して引いている部分は、dCountは整数であるため小数化するための細工です。
ここには、一周360度をdCountで分割したときの角度が入ります。
ループにてangleVを0.0から開始してdivAngleずつ増やしていきます。
「xPos = r * cos(angleV)」「zPos = r * sin(angleV)」で円周上の位置を計算しています。
これを球のX、Zに入れて半径50の球を配置しています。
これくらいになると、プログラムを使わないと難しくなりますね。
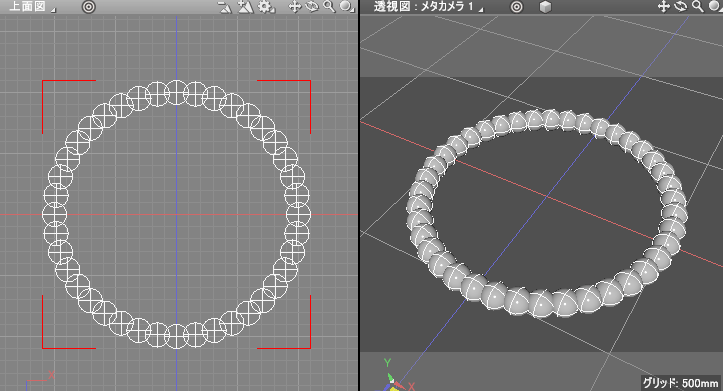
dCountを40とすると以下のようになりました。
sin波、cos波を描く
波の曲線を複数の球を使って作成します。
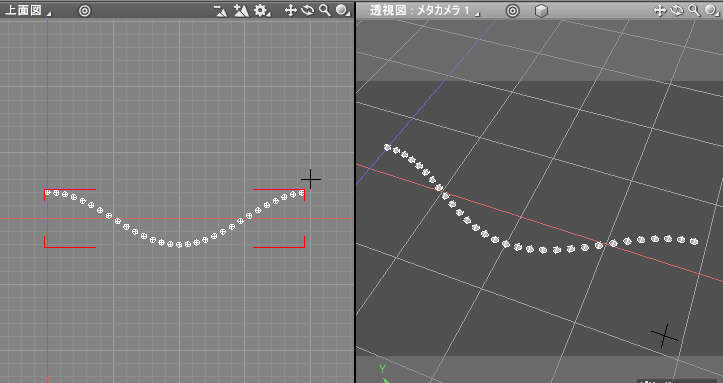
これはブロックUIプログラミングツールで以下のようにブロックを構成しました。
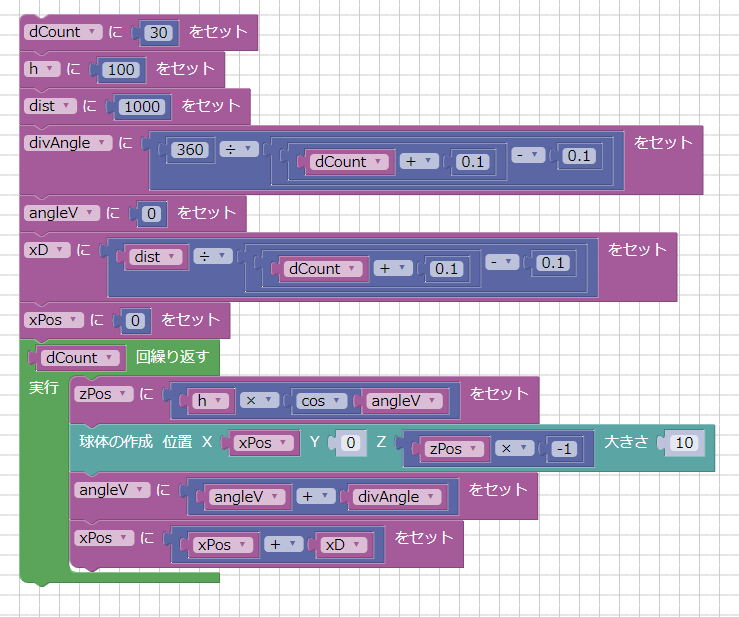
今度は円状ではなく、直線上にcos値の変化を配置しています。
「dCount」に配置する球の個数、「h」はZ軸方向の配置位置の最大、「dist」はX軸方向の配置位置の最大です。
「divAngle = 360 ÷ (dCount + 0.1 – 0.1)」で小数値として三角関数に渡す角度値を計算しています。
「xD = dist ÷ (dCount + 0.1 – 0.1)」でX軸方向の移動量を計算しています。
ループにて、angleVをdivAngleごと、xPosをxDごとに増加させています。
ループ内の「zPos = h * cos(angleV)」で波の高さを計算しています。
(xPos, 0, -zPos)を中心に球を作成することで、ここではcos値による波の変化を確認できます。
なお、Z値は上面図では下方向にプラスになるため、マイナスをかけて上方向がプラスとなるようにしています。
ここで、「divAngle = 1000 ÷ (dCount + 0.1 – 0.1)」のように360から1000にすると、波の数が増加します(360で一周期分になります)。
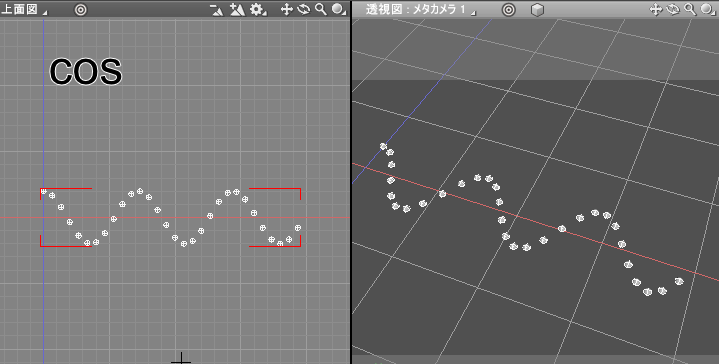
「zPos = h * sin(angleV)」にすると以下のようになりました。
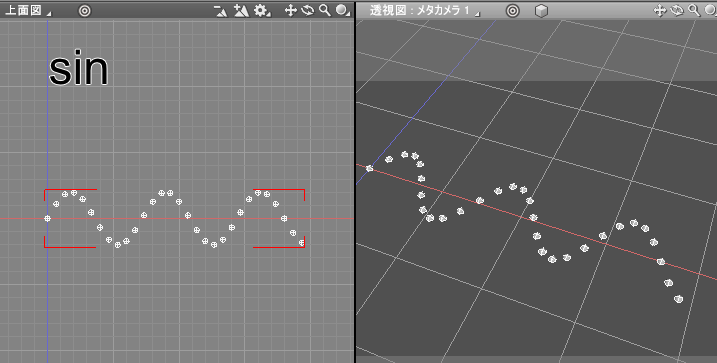
X=0(角度0)の位置で高さが1.0になっているのがcos、高さが0.0になっている(原点から球は配置されている)のがsinになります。
このような波は、周期や高さ(幅)を変更して複数の波を組み合わせることで、より複雑な波形を表すことができます。
今回はここまでです。
三角関数についての説明でした。
次回は上級編の最終回として、ブロックUIプログラミングツールを使って作品を作ります。
また、プログラミングではブロックUIプログラミングツールのようなツールを使って書くということはなく、
プログラミング言語を使うことになります。
少しだけですが、Pythonプログラミングについても書いていく予定です。