![]()
- 座標と座標系
- 位置や距離の単位 (メートル法)
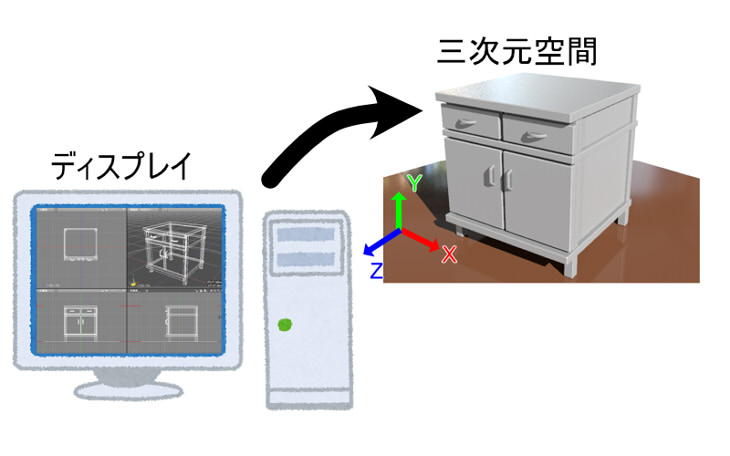
コンピュータ上で動くShade3DやブロックUIプログラミングツールは、ディスプレイ越しの二次元空間で操作を行います。
内部的には現実世界と同じような三次元の空間を持っています。
この空間を「シーン」と呼びます。
※ 「シーン」は3DCG(三次元コンピュータグラフィックス)の用語です。
3DCGでは三次元の考え方の知識がないと話を進めにくいため、今回は座標や二次元/三次元/単位について説明していきます。
なお、小学校学習指導要領の範囲に合わせて目標対象/学年の説明を入れていますが
これは変更される場合もあるため、ある程度の目安とお考えくださいませ。
座標とは ?
空間内の位置を表すために「座標」を使用します。
まずは算数で使われる二次元空間について説明し、三次元空間の考え方に触れていきます。
算数で使われる座標 (二次元の場合)
算数で使われる座標は、横方向をX、縦方向をYと表した二次元空間を使用します。
この「二次元」は紙やコンピュータのディスプレイのような平面上の空間を指します。
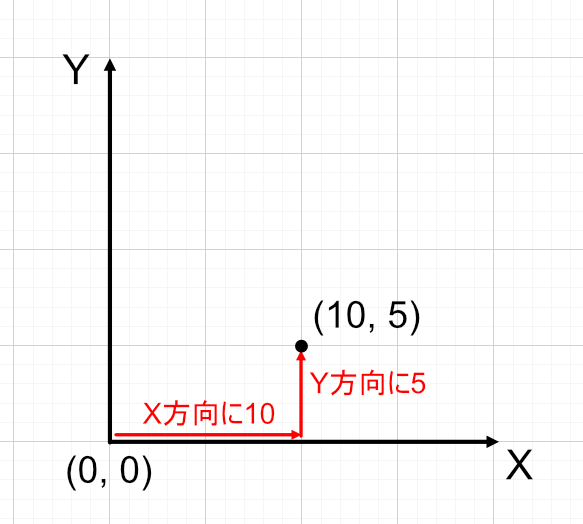
左下を(0,0)としています。これは「原点」と呼ばれます。
上画像の場合、右に10移動し上に5移動します。このときの位置は(10, 5)となります。
また、移動方向は横軸をX、縦軸をYとしています。
この座標により、この2次元空間上の位置を決めることができるようになります。
この軸を配置して位置を定めることができる仕組みを「座標系」と呼びます。
プラスとマイナス
※ プラスやマイナスの「符号」は中学校の範囲になります。
X=0やY=0よりも小さい、軸と逆向きの場合は「マイナス(-)」となります。
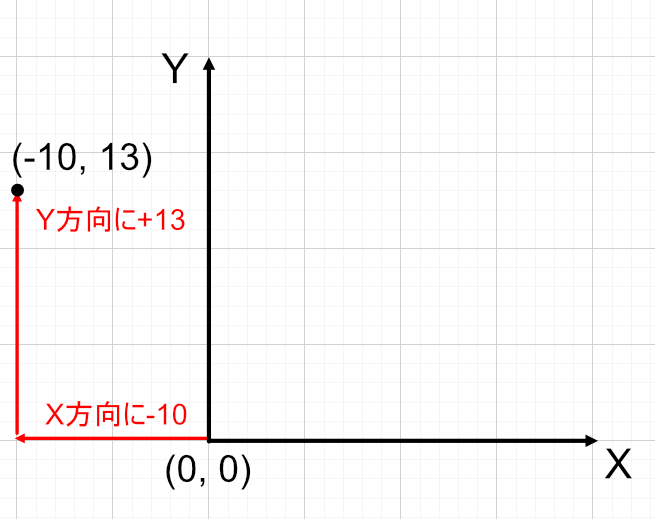
上画像の場合、左に10移動(右に-10移動と同じ意味です)し上に13移動します。このときの位置は(-10, 13)となります。
「プラス(+)」は省略されており、(-10, 13)と(-10, +13)は同じ意味になります。
算数で使われる座標 (三次元の場合)
※ 三次元の考え方については、小学校高学年の範囲になります。
「三次元」は、「二次元」に対して「高さ」方向の軸が加わった空間を指します。
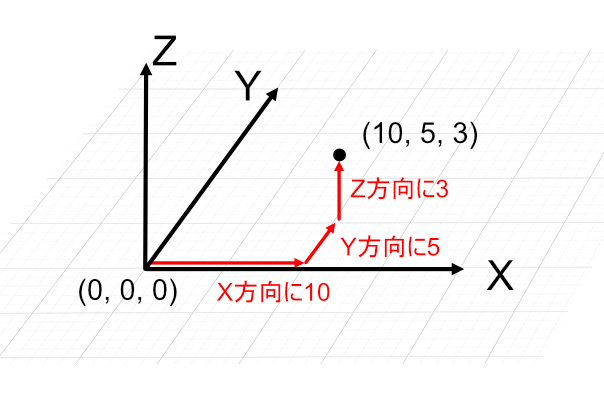
上画像の場合、右に10移動し上に5移動、さらに高さ方向に3移動します。このときの位置は(10, 5, 3)となります。
Shade3Dで使われる座標
Shade3Dで使われる座標は、初期状態では算数で使われる座標とは異なる軸の名前、軸の向きとなっています。
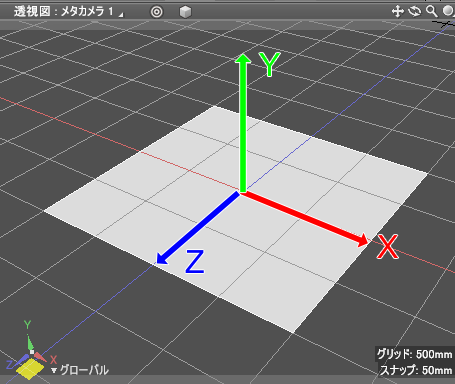
平面はX軸とZ軸で構成され、Z軸は手前に伸びます。
また、高さ方向はY軸となります。
Shade3Dの場合は、メインメニューの「編集」-「環境設定」を選択し、「座標系」の「上方向の軸」を「Z軸」に変更することで、座標系を切り替えることができます。
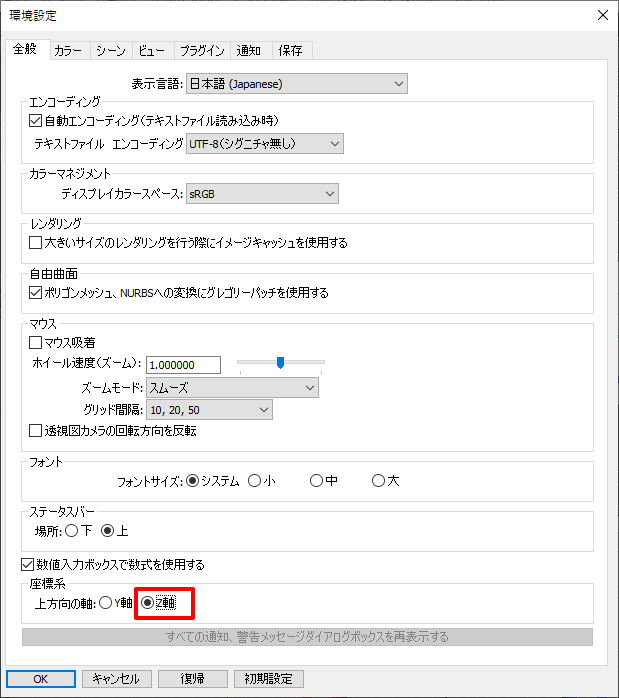
「上方向の軸」の切り替えは、Shade3D Standard/Professional版の機能になります。
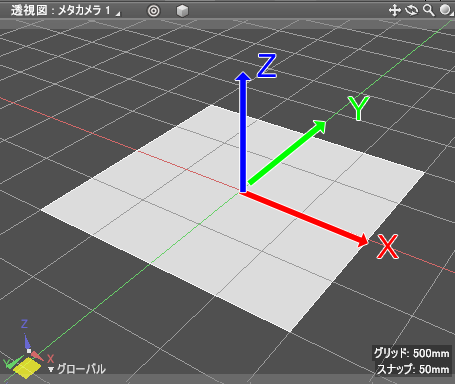
この場合、平面はX軸とY軸で構成され、Y軸は奥に伸びます。
また、高さ方向はZ軸となります。
ただし、ブロックUIプログラミングツールは「上方向の軸」がY軸となるのを前提にしている動作のため、初期状態(「上方向の軸」がY軸)に戻して説明していきます。
3DCGツールでは、この座標系が異なる場合が多いです。
どちらが正しいというものではなく、用途によって使用する座標系は異なります。
CAD用途(最終的に建物や工業製品などを作るための設計を、コンピュータ上で行うソフトウェア)の場合はZ軸が上向き、
ゲームなどのリアルタイム用途の場合はY軸が上向きとなっている場合が多いかもしれません。
ただし、ソフトウェア(ツール)によって座標系が異なる面もあるため、これらは混在しています。
単位
※ 「メートル法」の考え方については、小学校高学年の範囲になります。
現実世界は三次元の空間になり、もう一つの位置や距離を示す物差しとして「単位」が存在します。
Shade3Dの場合、標準の単位としてmm(ミリメートル)を使用します。
距離の単位は、以下のような関係性になります。
- mm(ミリメートル) x 1000 = m (メートル)
- m (メートル) x 1000 = km (キロメートル)
距離に限らず、「ミリ」は1/1000倍、「キロ」は1000倍、の表現を行います。
では、この座標と単位について、改めてブロックUIプログラミングツールとShade3Dを使って確認していきます。
ブロックUIプログラミングツールを使って、指定の位置に円を配置
ブロックUIプログラミングツールのウィンドウを表示し、
ツールボックスで「形状」を選択。
「円の作成」を選択します。
このときの球体の中心位置としてX=1000、Y=0、Z=500、半径50を指定します。
単位は「mm(ミリメートル)」となります。
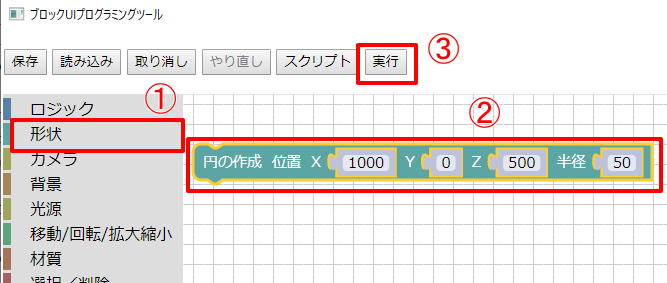
ボタンエリアで「実行」ボタンを押して、形状を生成します。
(X, Y, Z) = (1000, 0, 500)の位置に半径50(mm)の円が配置されました。
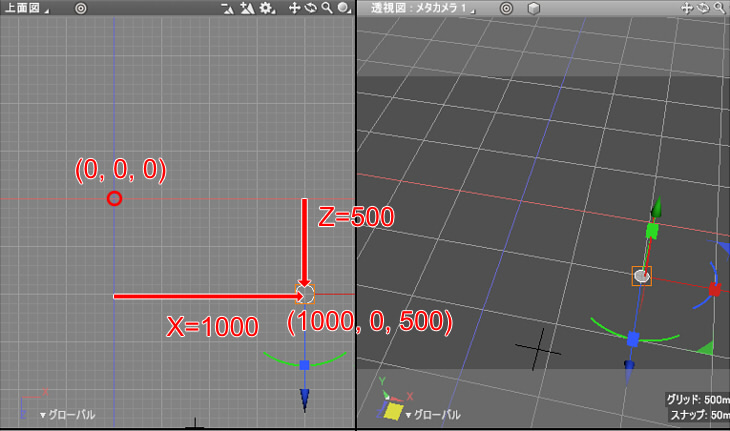
ここではY=0としているため、上面図で見ると分かりやすいかと思います。
なお「算数」での座標と異なり、上面図上で見たときはY軸ではなく「Z軸下向きにプラスとなる」ことに注意してください。
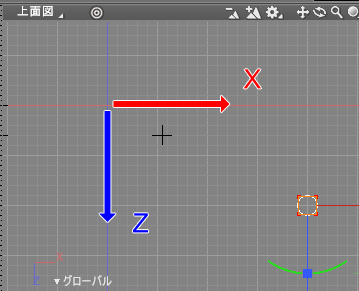
Shade3Dでの座標位置の確認
マウスカーソルをShade3Dの図形ウィンドウ上で移動させると、
ウィンドウ下のステータスバーに座標値が表示されます。
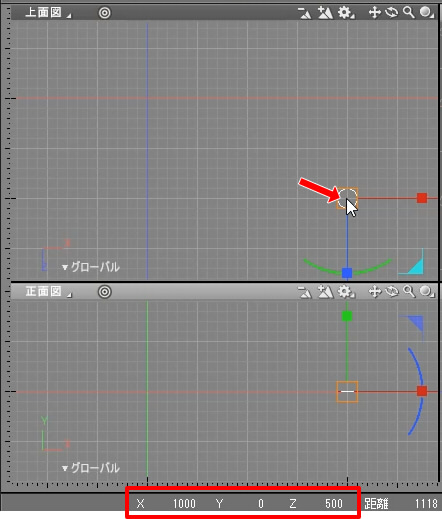
このステータスバーは環境設定ウィンドウで上に位置移動させることができます。
円の要素
円は、「中心」と「半径」で表されます。
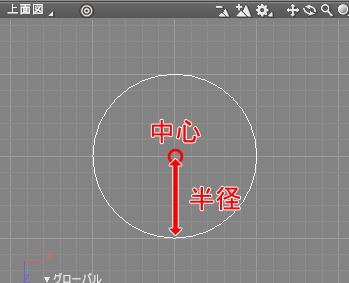
このように、座標は位置だけでなく大きさの表現でも使用されます。
ブロックUIプログラミングツールを使って、座標指定で四角形を配置
座標について理解がある程度進みましたので、四角形を座標値を使って表現してみます。
ブロックUIプログラミングツールのウィンドウを表示し、
ツールボックスで「形状」を選択。
「点の位置を指定して線を作成」を選択します。
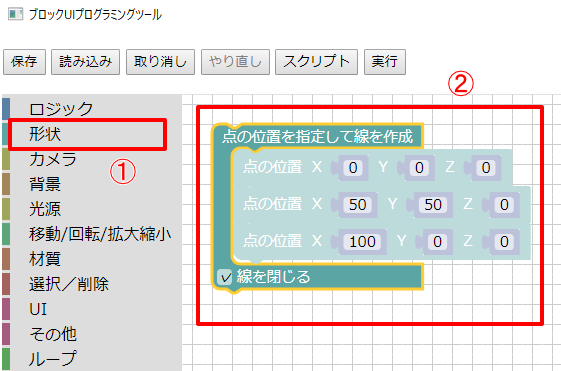
これは、特定の座標をつなぐことにより形状を作成する機能です。
「線を閉じる」チェックボックスをオンにすることで、始点と終点は閉じられます。
これで四角形を描いてみましょう。
ツールボックスで「形状」を選択し、「点の位置」を配置します。

これを4回分繰り返します。
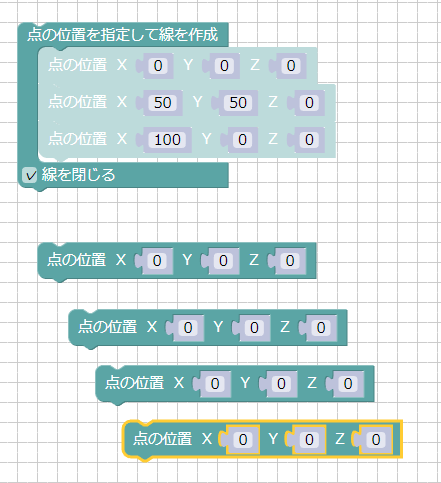
ブロックを選択して右クリックし「複製」を選択することで指定のブロックを複製することもできます。
このブロックをドラッグし、「点の位置」4つ分を連結します。
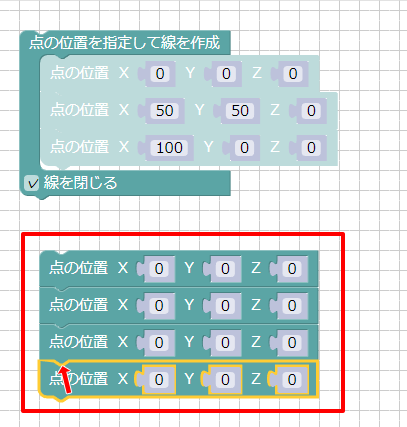
この4つの点に対して座標値を指定します。
座標の割り当てについては、Shade3Dの上面図で見ながら確認するのが分かりやすいかと思います。
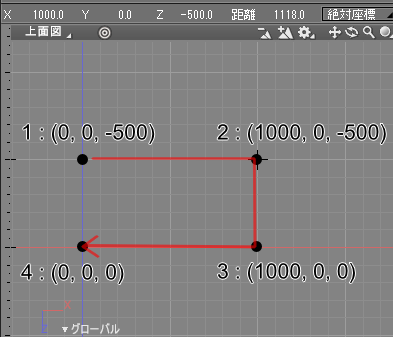
以下のように4つの座標を時計回りにつなぐと四角形ができます。
- 1 : (0, 0, -500)
- 2 : (1000, 0, -500)
- 3 : (1000, 0, 0)
- 4 : (0, 0, 0)
この数値を、ブロックUIプログラミングツールの「点の位置」のXYZで指定します。
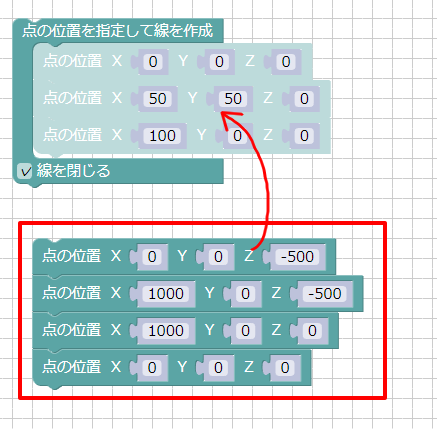
「点の位置」の一番上のブロックを選択して「点の位置を指定して線を作成」の中にドラッグします。
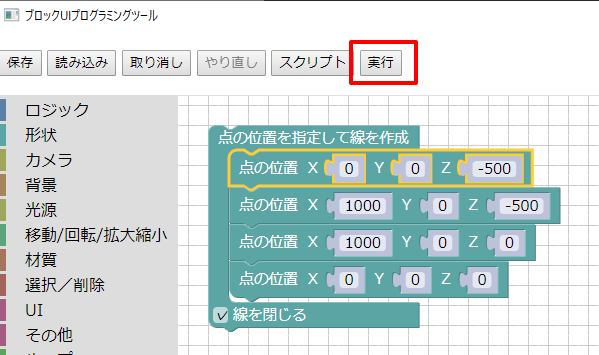
これで、「点の位置を指定して線を作成」で位置を指定した形状を作成できるようになります。
「実行」ボタンを押すと、Shade3Dでは以下のように四角形が配置されました。
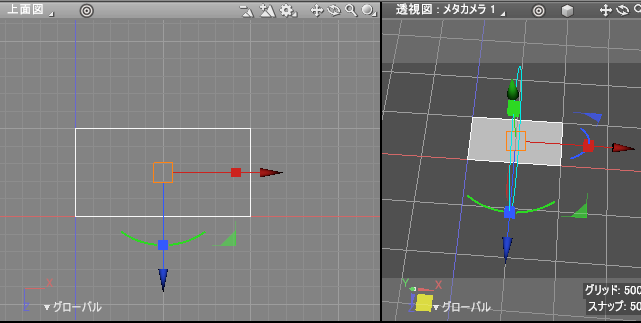
階段状の形状を作成
では、今回の問題です。
[問題 1] 以下のような階段状の形状は、いくつの座標で作成できるでしょうか ?
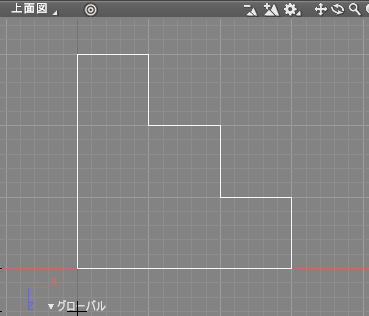
[答え 1] 8点
以下のような8つの座標で作成できます。
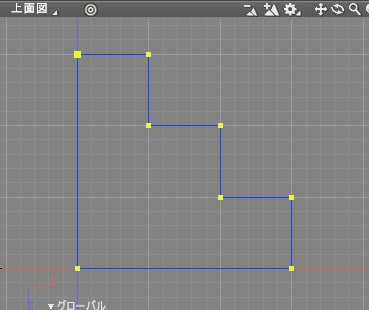
[問題 2] この形状の座標値を求めてみましょう。座標は時計回りに指定します。
上面図で見て、左下を原点(0, 0, 0)、500 mm の距離で階段状になっているものとします。
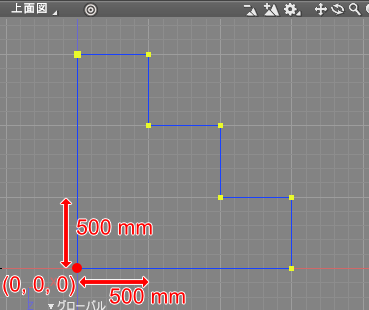
[答え 2] 左上から時計回りに座標を与えると以下のようになります。
- 1 : (0, 0, -1500)
- 2 : (500, 0, -1500)
- 3 : (500, 0, -1000)
- 4 : (1000, 0, -1000)
- 5 : (1000, 0, -500)
- 6 : (1500, 0, -500)
- 7 : (1500, 0, 0)
- 8 : (0, 0, 0)
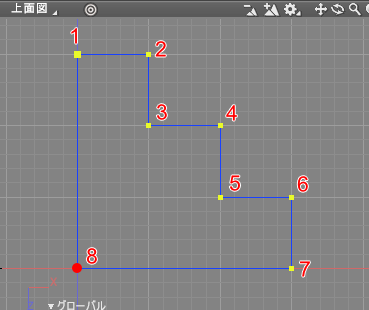
これらの座標は、上面図上でマス目を見て位置を確認していくのが手っ取り早いかと思われます。
これにより、座標に慣れるようにしましょう。
[問題 3] ブロックUIプログラミングツールを使ってこの階段形状を作成しましょう。
[答え 3] 以下のようにブロックを組み合わせます。
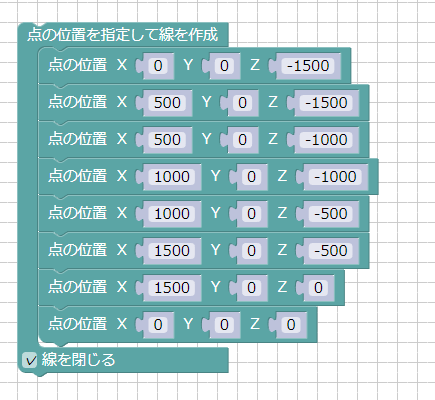
実行すると以下のようになりました。

今回はここまでです。
座標や単位についての理解、ブロックUIプログラミングツールで座標を指定した形状を作成するという内容でした。
座標や三次元を扱う場合、小学校低学年の範囲ではカバーしきれない部分が出てきます。
少しフライングしていますが、「初級編」で座標や三次元について最低限必要な知識も盛り込むようにしました。
次回は初級編の最後、四則演算や計算式について説明していく予定です。