[中級] 符号/分数/小数/面積/円周率

ブロックUIプログラミングツールの中級編、今回は符号/分数/小数/面積/円周率について書いていきます。
符号/分数/小数/円周率は算数の範囲になり、3DCGでもよく使われます。

符号（プラスとマイナス）

※ プラスやマイナスの「符号」は中学校の範囲になりますが、説明の流れで必要なためここで解説しておきます。

今までの説明では、数値はプラスのみ使用していました。
0を中心に+1していくごとに+1、+2、+3、+4 となります。なお、「+」（プラス）は省略できます。
逆に、0を中心に1を引いていくと、-1、-2、-3、-4 となります。数値の前に「-」（マイナス）を付けます。

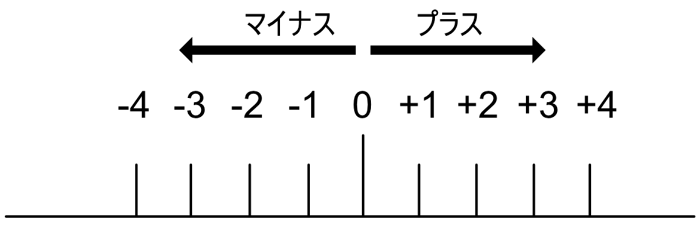
この「+」や「-」は「符号」と呼びます。
プラスの値を「正の値」、マイナスの値を「負の値」とも呼びます。

符号の性質

引き算の「4 – 5」の場合、「4 + (-5)」と置き換えることができます。
これは「+4と-5を足し算する」と同じ意味です。
また、「-5 + 4」の場合は置き換えて「4 – 5」と計算することができます。
四則演算で計算としてのプラスマイナスと符号としてのプラスマイナスが混在する場合、
「A + (-B)」は「A – B」、「A – (-B)」は「A + B」と置き換えることができます。

かけ算で「4 x (-5)」とした場合、結果は-20となります。
「(-4) x 5」とした場合も、結果は-20となります。
「(-4) x (-5)」とした場合、結果は20となります。
「マイナス x プラス」の計算はマイナス値となり、「マイナス x マイナス」の計算はプラス値になります。

割り算で「6 ÷ (-2)」とした場合、結果は-3となります。
「(-6) ÷ 2」とした場合も、結果は-3となります。
「(-6) ÷ (-2)」とした場合、結果は3となります。
割り算の場合の符号はかけ算の時と同じで、
「マイナス ÷ プラス」「プラス ÷ マイナス」の計算はマイナス値となり、「マイナス ÷ マイナス」の計算はプラス値になります。

[問題 1] ブロックUIプログラミングツールを使って「-40 – 20 x (-3) + 80」を計算してみましょう。結果はいくつになるでしょうか。

[答え 1] 100

これはひっかけ問題です。-20と答えたら間違いです。
まず、四則演算はかけ算と割り算を先に行います。「20 x (-3)」を先に計算します。
結果は「-60」です。
式を置き換えて「-40 – 20 x (-3) + 80」は「-40 – (-60) + 80」となります。
-40から-60を引く計算は「-40 + 60」と置き換えできます。ここで符号を忘れてしまうと計算間違いを起こします。
式は「-40 + 60 + 80 = 100」と計算できます。

これをブロックUIプログラミングツールで計算します。
ツールボックスで「計算」を選択し、計算と数のブロックを配置します。

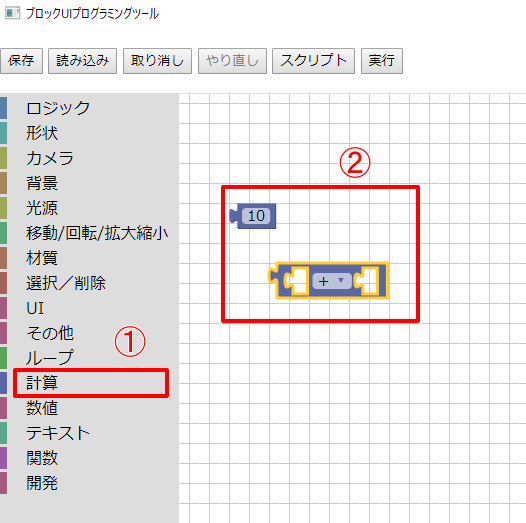
数のブロックを複製し、以下のように「20 x (-3)」を組み合わせました。

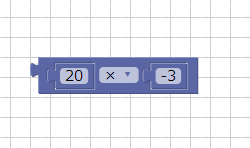
計算のブロックを新しく2つ配置し、「-40 – 20 x (-3)」を組み合わせ。

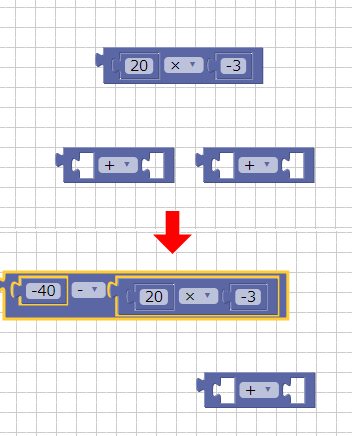
「-40 – 20 x (-3)」に80を足し算。

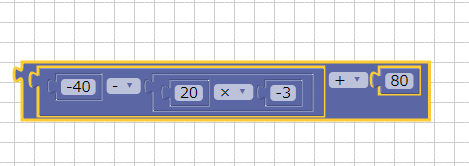
ツールボックスの「その他」から「メッセージを表示」ブロックを配置します。

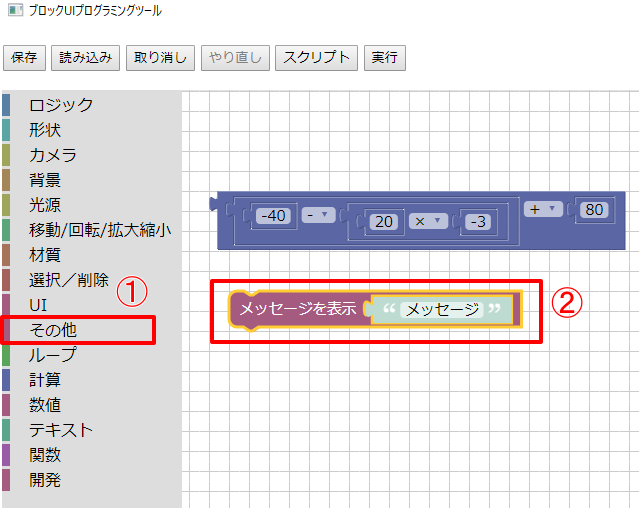
以下のように、数値の結果をメッセージウィンドウに表示するようにしました。

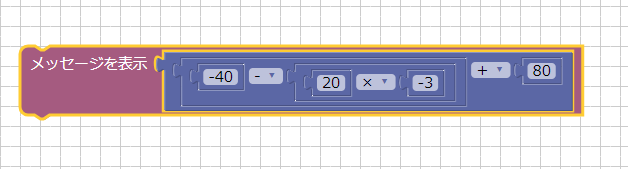
これを「実行」すると、メッセージウィンドウで「100」と表示されます。

割り算の符号を分離

割り算での符号は少し分かりにくいですので、補足しておきます。
「30 ÷ (-5)」の計算は「30 ÷ (5 x (-1))」と置き換えできます。
かけ算と割り算は前から順番に計算できるため、「(30 ÷ 5) x (-1) = 6 x (-1) = -6」と計算できます。
このように、符号を分離して考えると計算しやすいかもしれません。

小数

今までは数値については「整数」で説明していました。
「整数」とは、-10、0、1、15、100などのような数値です。
一方「小数」は-10.3、0.5、0.28のような「小数点」以下の値を持つ数値です。
この0と1の中間の数値は0.5となります。
1と2の中間は0.5です。

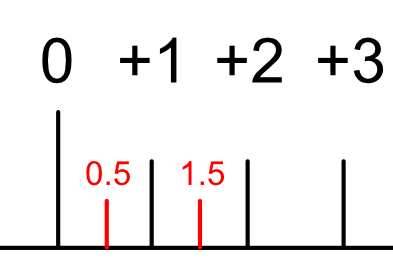
この「0.5」と表記したときの「.」を「小数点」、「.」より右を「小数部」と呼びます。
「.」より左は「整数部」です。
「小数」（小数の値）と書いた場合は、0.5や0.28などの整数部と小数部を含む数値表現を指します。

10進数

以下は、0から1の間を10等分した表現です。

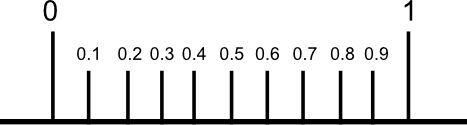
算数/(中学校の)数学で扱う数値は「10進数」と呼ばれています。
これは、1を10倍したら10、10を10倍したら100、1を1/10倍(これは0.1倍と同じ)したら0.1となります。
10進数は「10」で桁上がりする表現です。

コンピュータの世界では、内部的にはこの10進数では扱われていません。
コンピュータでは2進数が根底にあります（もっとも小さな単位では、0と1の電気信号で扱うため）。
ただ、そのままでは人間が扱いにくいため、2進数から16進数にし、さらに10進数の計算ができるようにハードウェアとしてプログラムされています。
この部分はもっと専門の知識になってきますので、ここでは説明を省きます。

小数を分数で理解する

割り算の「7 ÷ 5」の計算では、「1 余り 2」という表現をしています。
これを小数値で計算すると「1.4」となります。
計算する場合は、「(7 x 10) ÷ 5 ÷ 10」のように、7を10倍して最後に10で割ると理解しやすいかもしれません。
この計算では「(7 x 10) ÷ 5 = 70 ÷ 5 = 14」となり、「14 ÷ 10 = 1.4」と計算しやすいです。

文章で書くと分かりにくいため、ここで分数を使って表現してみましょう。
「7 ÷ 5」を分数で表すと以下のようになります。

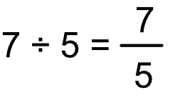
文章で書くと「5分の7」です。
さらに、以下のように分解できます。

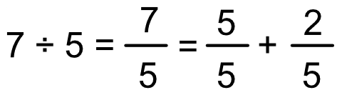
「5分の5」は1のため、以下のようになります。

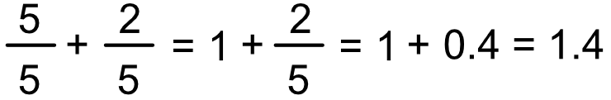
もし、整数と余りで表現する場合は、「1 と 5分の2」から「1 余り 2」が導き出せるのが分かりますでしょうか。
「5分の2」は小数に変換する場合、分母と分子を10倍すると理解しやすいです。

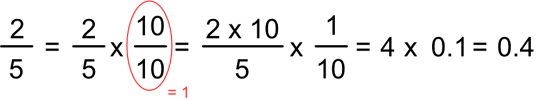
これで、数値を細かい値まで表現できるようになりました。
符号/分数/小数は基礎部分になるため、先に説明しておきました。

面積の計算

「面積」は面の大きさ/量のことを指します。
3DCGでは面積についてはあまり出てきません。Shade3Dでも二次元での面積を計算する機能はありません。
※ CADなどの設計用途では面積計算は出てきます。

ただ、内部的な計算（光の計算やモデリングなど）では使用されています。
また、このチュートリアルで解説している「算数」では必須項目になっています。
後述する円周率を使った計算で部分的に使用しているのもあるため、ここで説明することにしました。

四角形の面積

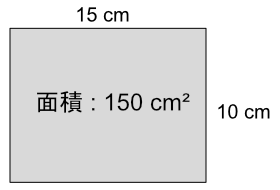
四角形の面積は「横の長さ x 縦の長さ」で計算できます。
以下の画像は、横に15、縦に10となっています。
この時の面積は「15 x 10 = 150」と計算できます。

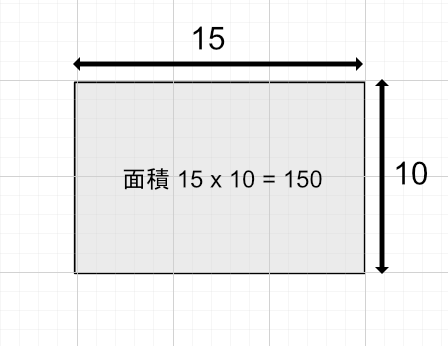
これは、上画像のマス目の1つを面積1としたときのマスの合計を計算するのに相当します。

平行四辺形の面積

四角形の上辺を水平にずらした表現は「平行四辺形」と呼ばれます。
この面積は四角形の時と同じで「横の長さ x 縦の長さ」で計算できます。

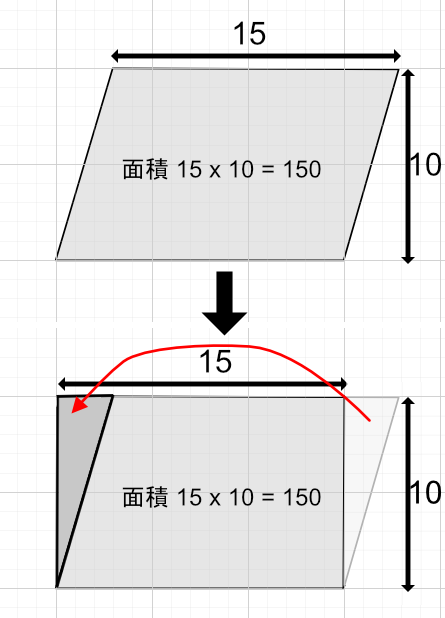
この面積の計算は、四角形からはみ出した部分を切り取り、反対側に合わせることで理解しやすくなります。

二等辺三角形と面積

二等辺三角形とは、三角形を表現するときに2つの辺が同じ長さの三角形です。

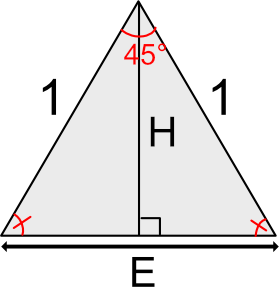
また、底辺の角の角度は同じになります。
この三角形は、底辺の中央から頂上の角に伸ばした垂線を境にして2つの「直角三角形」で構成できます。
このときの二等辺三角形の面積は、底辺の長さE、高さHのときに、「(E x H) ÷ 2」で計算できます。
面積は垂線で三角形を2つに分けて組み替えると理解しやすいです。

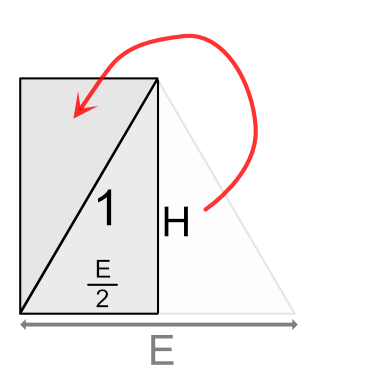
片側の直角三角形を回転して移動すると、長方形になります。
これで「(E ÷ 2) x H」で面積が求まります。
この面積の計算式は、普通の三角形でも成り立ちます。
「底辺 x 高さ ÷ 2」が三角形の面積の計算式になります。

面積の単位

距離の単位がセンチメートル(cm)の場合、面積は「cm²」のように表現します。
読みは「平方センチメートル」です。

距離の単位がメートル(m)の場合、面積は「m²」のように表現します。
読みは「平方メートル」です。

円と円周率

二次元での長方形、立体の直方体/立方体は、線分の組み合わせの面で表現できます。
円や球は曲線を含んでいます。
曲線表現として一番簡単な例として円を考えます。
円は中心と半径で表現されます。
以下の画像は半径1の円の表現です。

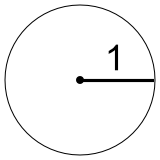
半径1の円のぐるっと一周の長さ（円周）はいくつになるでしょうか?

考え方は、円を三角形で構成するようにしてその1辺の長さを加算していきます。
以下の画像では、円を8等分しています。角度は360 ÷ 8 = 45°ごとです。

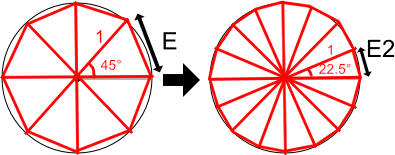
2辺の長さが1の二等辺三角形の集まりと考えます。
このときの二等辺三角形の底辺の長さをEとした場合、「E x 8」が円周の長さになります。
16等分した場合は角度は22.5° (360 ÷ 16 = 22.5)ごとになります。
このときの底辺の長さをE2とした場合、「E2 x 16」が円周の長さになります。

このように分割数を増やしていくことで、より正確な円周に近づいていくことになります。
なお、曲線の場合はいくら細かく分割しても完全に正確な値は求まりません。
「近似」として近い値を答えとしています。

このときの二等辺三角形の底辺の長さは、角度と2辺の長さ（= 1）から計算できるのですが、その場合は中学校レベルの知識がいるのでここでは説明しません。

最終的には「半径1の円の円周の長さ = 6.2831853…」のように割り切れない値が出てきます。
この円の円周の計算式は「2 x 半径 x 3.14 = 直径 x 3.14」で計算できます。
この「3.14」は「円周率」と呼ばれます。記号では「π」(パイ)と書かれることが多いです。
半径Rの円の場合、円周の計算式は「2 x π x R」と表現されます。
「円周率」は割り切れない数値で「3.1415926535…」とずっと続きます。
算数では小数点以下2ケタまでで表現し「π = 3.14」としています。
円周率が本当に3.14かどうかについては上級編で改めて解説予定です。
この円周率は3DCGではよく使われます。

この半径Rの円周の計算式は「2 x π x R」、といった表現は「公式」と呼ばれます。
公式を何も考えずに暗記して覚えてもよいのですが、なぜそのような式になったのかを理解していくほうが後々理解が深まります。
「算数」の段階ではこの公式を解くための知識が足りないため、今はそういうものだと暗記しておきましょう。

円の半径から円周の長さが計算できました。
では、面積はいくつになるでしょうか？

円と面積

[問題 2] 半径1の円の面積を計算しましょう。

[答え 2] 半径1の円の面積は「3.14」となります。

これは先ほど説明した円を二等辺三角形で分割する方法から導き出します。
半径1の円の円周は「1 x 2 x π = 2π = 6.28」と計算できます。
円を45°ごとに8等分する場合、底辺の長さは「6.28 ÷ 8 = 0.785」となります。
※ この0.785は実際は線分ではなく曲線になります。

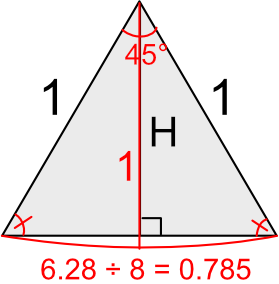
上記の計算で三角形の高さHを強引に1とした場合（分割数が増えると限りなく1に近づくことになり、曲線も直線に近づきます）、この三角形の面積は「底辺 x 高さ ÷ 2」より「0.785 x 1 ÷ 2 = 0.3925」となります。
これが8個分なので「0.3925 x 8 = 3.14」と計算できます。

半径Rの円の場合、円周は「2 x π x R = 6.28 x R」。
8等分したときの二等辺三角形の底辺の長さは「6.28 x R ÷ 8」。
1つの三角形の面積は「(6.28 x R ÷ 8) x R ÷ 2」。
これが8個分なので「(6.28 x R ÷ 8) x R ÷ 2 x 8 = 3.14 x R x R」と計算できます。
結果として、円の面積の計算式は「π x R x R」で求まります。
円を8等分ではなく16等分とした場合もこの式は成立します。
この分割数を増やしていくとより正確な値に近づきます。
この計算途中の式を見ると「÷ 8」と「x 8」があり、これは計算すると「x 1」となり数値に1をかけても結果は変わらないため、分割数自身を式から消すことができます。

ブロックUIプログラミングツールで確認

では、ブロックUIプログラミングツールで今回説明したことをいくつか確認してみましょう。

[問題 3] 原点を1つの頂点とした300(mm) x 150(mm)の四角形を作成しましょう。
X軸方向に300(mm)、Z軸方向に150(mm)とします。

[答え 3] 以下のようなブロックの組み合わせになります。

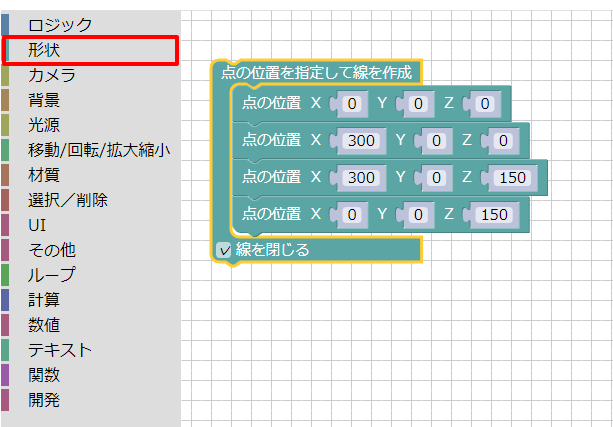
ツールボックスの「形状」で「点の位置を指定して線を作成」「点の位置」を配置し、組み合わせました。
実行すると以下のようになります。

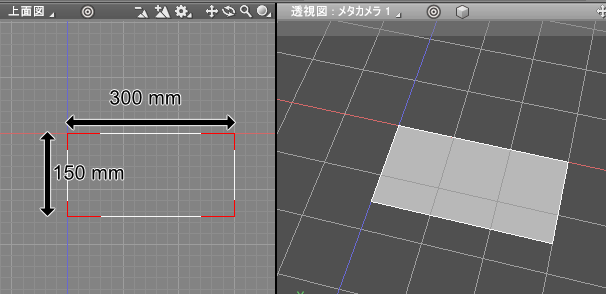
[問題 4] [問題 3]で作成した四角形の面積を計算しましょう。単位も記載するようにしてください。

[答え 4] 45000 mm²

300 x 150 = 45000で計算できます。
簡単ですので暗算で計算してしまってもかまいません。
暗算する場合は、「(3 x 100) x (15 x 10) = 3 x 15 x (100 x 10) = 45 x 1000 = 45000」と区切りのいい10や100をいったん分離して、
並べ直して計算すると分かりやすいです。

ブロックUIプログラミングツールで計算して結果を表示するには、以下のように組み合わせます。

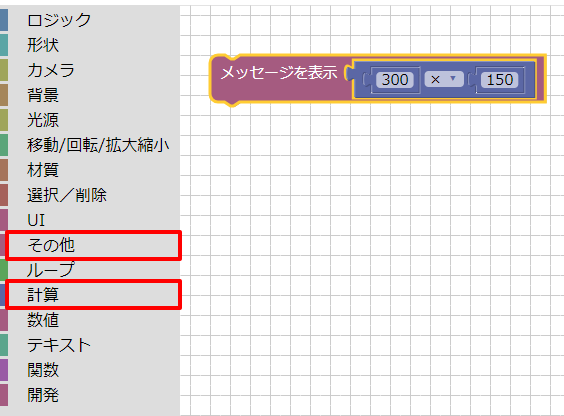
ツールボックスの「計算」から計算と値のブロックを配置して計算を「300 x 150」とし、
「その他」で「メッセージを表示」ブロックを配置してその中に入れます。

[問題 5] [問題 4]で計算した面積の単位を平方センチメートル、平方メートルにして表現しましょう。

[答え 5] 450 cm²、0.045 m²

計算するときは、まず長方形の幅と高さを300(mm)から30(cm)、150(mm)から15(cm)に単位変換します。
ミリメートルからセンチメートルに変換する場合は、値を10分の1倍します。
面積は「30 x 15 = 450 cm²」と計算できます。

ミリメートルからメートルに変換する場合は、値を1000分の1倍します。
300(mm)から0.3(m)、150(mm)から0.15(m)に単位変換します。
面積は「0.3 x 0.15 = 0.045 m²」と計算できます。

[問題 6] 300(mm) x 150(mm)の四角形内に収まるように、半径50(mm)の円は何個入るでしょうか?
四角形内に円を配置してみましょう。

[答え 6] 3つ入ります。

ブロックUIプログラミングツールで以下のようにブロックを組み合わせました。

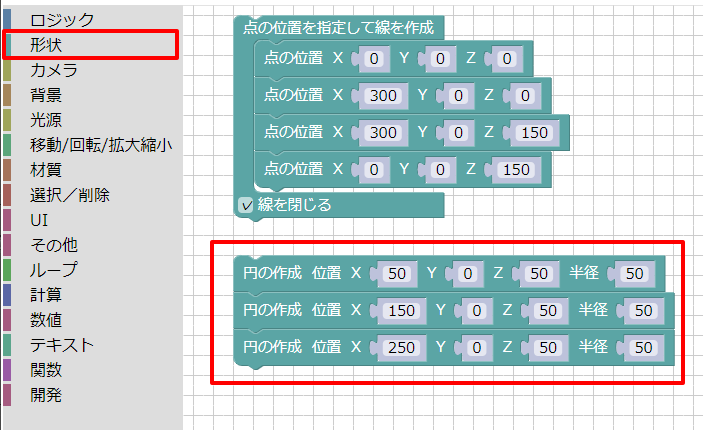
ツールボックスの「形状」で「円の作成」を配置し、(50, 0, 50)を中心として、X軸方向に100加算しながら半径50の円を配置します。
実行すると以下のようになります。

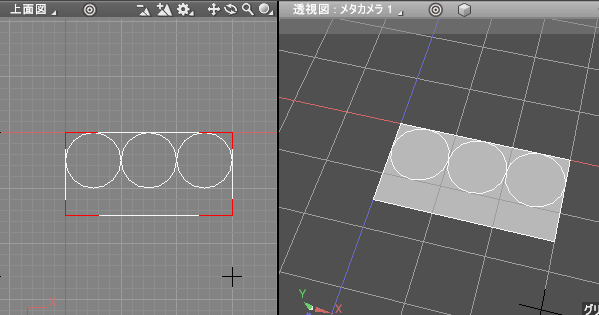
[問題 7] 300(mm) x 150(mm)の四角形から、[問題 6]で配置した半径50(mm)の円を引いた残りの面積はいくつになるでしょうか ?

[答え 7] 21450 mm²

300(mm) x 150(mm)の四角形の面積は「45000 mm²」。
半径50(mm)の円の面積は「π x R x R = 3.14 x 50 x 50 = 7850 mm²」。
[問題 6]の結果3つの円が配置されているため「7850 x 3 = 23550 mm²」。
これらより、「45000 – 23550 = 21450 mm²」と計算できます。

今回はここまでです。
まだまだ算数の知識が多くなりますが、知識が増えていくとよりできることも広がっていくというのが体感できるかと思います。
また、小数や分数を行き来したり面積や単位の理解が深まると、理屈で計算できるというのがなんとなく見えてきます。
算数/（中学校での）数学でこの理屈がつながっているというのが見えてくると、論理的な理解につながります。
これはプログラミングと非常に近いかもしれません。

次回は、立体の「体積」やプログラムの第一歩である「変数」「構文」など、算数とは少し離れた説明をしていく予定です。