![]()
- 「面」「辺」「直角」「垂直」「平行」
- 立体について
今回から「ブロックUIプログラミングツール」の中級編に入ります。
中級編は小学校高学年の算数の範囲となります。
三次元空間と「立体」の説明に入ります。
3DのツールであるShade3D/ブロックUIプログラミングツールは三次元空間を理解しないと進まない箇所があったため、「[初級] 座標と単位」で三次元について説明を入れていました。
改めて説明していきます。
三次元空間
「[初級] 座標と単位」での三次元についての復習です。
今まではXY軸がある二次元空間の説明を行っていました。
これはスクリーンで見ると、横方向(X軸)と縦方向(Y軸)より位置を決定することができる空間です。
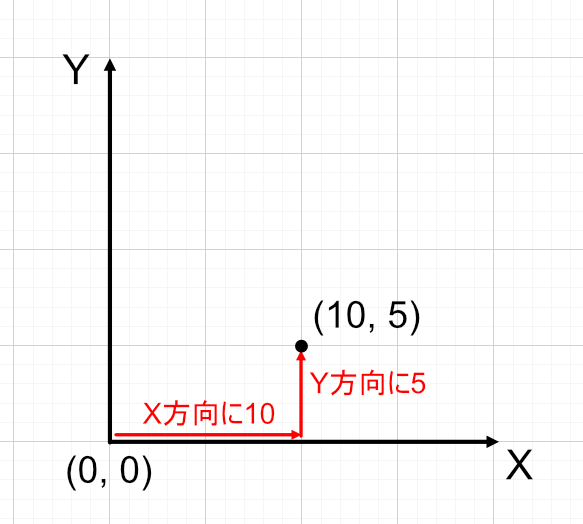
これに高さ方向のZ軸を加えることで三次元空間としています。
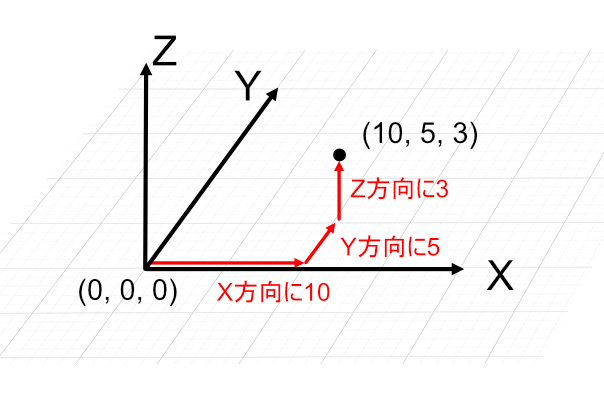
ただし、Shade3Dの場合は「座標系」として高さ方向がY軸となります。
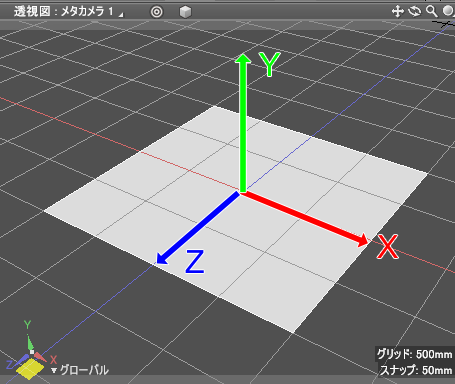
XYZの3つの値を与えることで、三次元空間上の位置を決めることができます。
現実世界での位置指定もこの三次元空間となります。
指定の位置に形状を配置
では、すでにShade3Dは三次元空間を持っていますのでここに形状を配置して確認していきましょう。
ブロックUIプログラミングツールのツールボックスで「形状」を選択。
「球体の作成」を選択します。
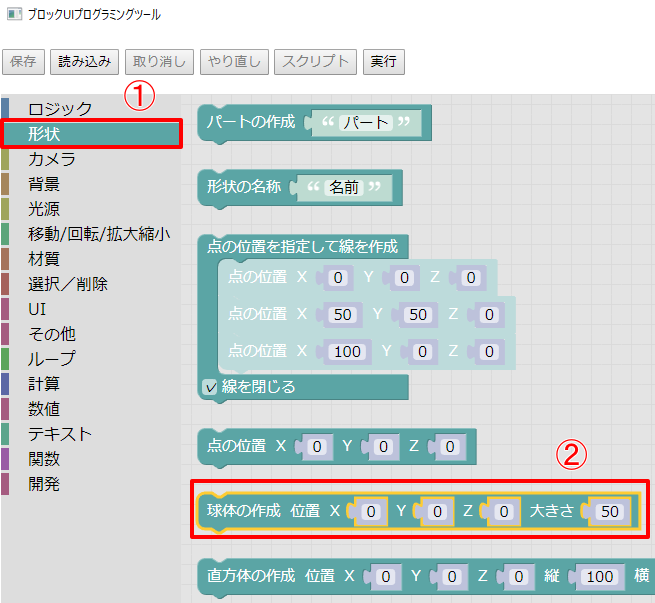
Xに500、Zに500を指定して「実行」ボタンを押すと、Shade3DのシーンにXYZ=(500, 0, 500)の位置に球が配置されました。
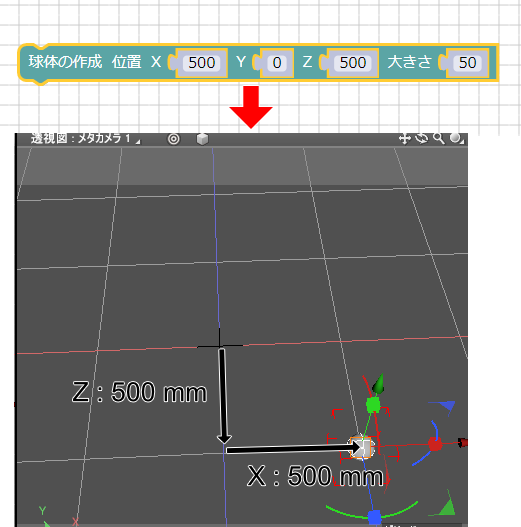
次にYに200を指定して「実行」ボタンを押すと、Shade3DのシーンにXYZ=(500, 200, 500)の位置に球が配置されました。
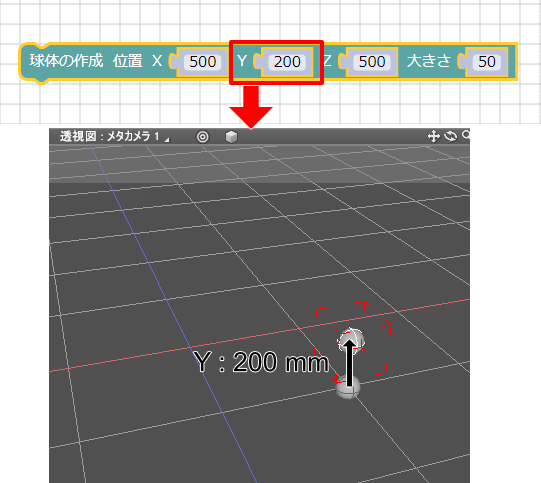
これは、XYZ=(500, 0, 500)の位置より高さ方向に200移動した位置です。
このような形で、三次元空間の位置はXYZを与えることで決めることができます。
立体
目に見えるモノは、どんなものでも「厚み」を持っています。
たとえば紙の場合、紙の上の文字や絵は二次元空間での表現になりますが、紙自身は薄いながらも厚みを持ちます。
三次元空間で表現すると高さがある状態です。
以下の画像は、平面に見えますが高さが1mmよりも小さい直方体です。

※ 1mm(整数値)よりも小さい値である「小数」については後々説明します。小数も中級編の範囲になります。
「立体」は、三次元で表現された形状です。
立体で使用する言葉
ここで「立体」で使用する「頂点」「辺」「面」「直角」「垂直」「平行」について説明しておきます。
四角形の場合、4つの「頂点」が存在します。
2つの頂点を結んだ線分を「辺」と呼びます。
「辺」で囲んで閉じた部分を「面」と呼びます。
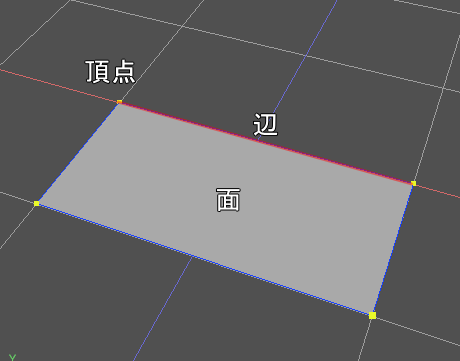
Shade3Dのような3DCGツールでも、この「頂点」「辺(Shade3Dでは「稜線」と呼んでいます)」「面」はもっとも基本の考え方として使用されます。
なお、2つの頂点を結んだ線は「線分」と呼ばれます。
2つの頂点が通過する線は「直線」と呼ばれます。

また、四角形の場合は4つの角の「角度」が90度になります。
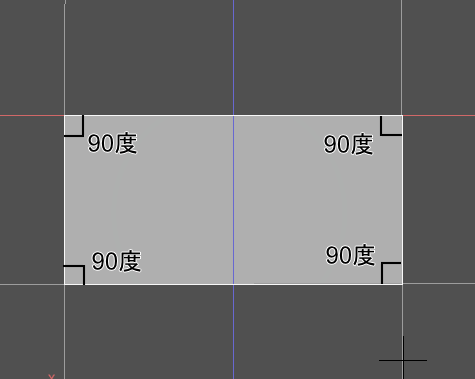
90度の角度のことを「直角」と呼びます。
「角度」は2辺を挟む角の大きさの単位になります。
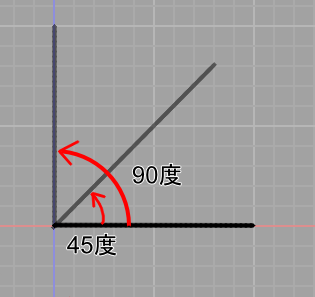
90度で直角になり、4つ分の直角で90 x 4 = 360で一回転となります。
角度については、円や円周率の説明のときに再度行うようにします。
ある辺または面から見て、90度の角度で配置される辺や面は「垂直」となっています。
以下の画像は、辺1と辺2は垂直の関係です。
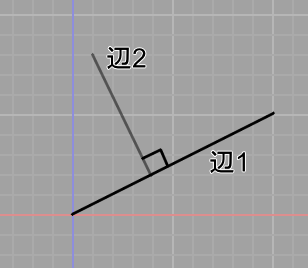
面と辺、面と面で作られる角度でも「垂直」の表現は使われます。
以下の画像は三次元空間で、面1と面2は垂直の関係です。面1と辺1も垂直の関係になります。

一方、2つの辺を伸ばしても交わらない場合、「平行」と呼ばれます。
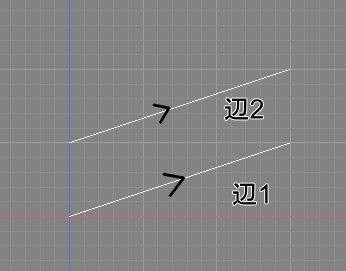
線分が平行な場合、記号では線の上に「>」を付けます。
複数の平行がある場合は「>>」「>>>」のように増やしていきます。
三次元空間での面同士でも平行な状態が存在します。

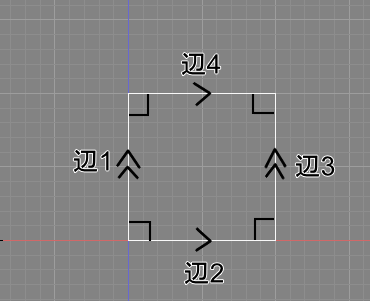
[問題 1] 正方形や長方形は4つの辺がありますが、何組の辺の垂直と平行があるでしょうか ?
[答え 1] 4組の垂直と2組の平行
垂直となる辺は、辺1と辺2、辺2と辺3、辺3と辺4、辺4と辺1、 の4つです。
平行となる辺は、辺1と辺3、辺2と辺4、 の2つです。
それでは、いくつかの立体の種類について説明していきます。
直方体と立方体
底面が四角形で、垂直に高さを持つ形状を「直方体」と呼びます。
「直方体」のうち、底面が同一の辺の長さの正方形で、高さも同じとなる場合は「立方体」と呼びます。
以下の画像は、左の立体が立方体です。
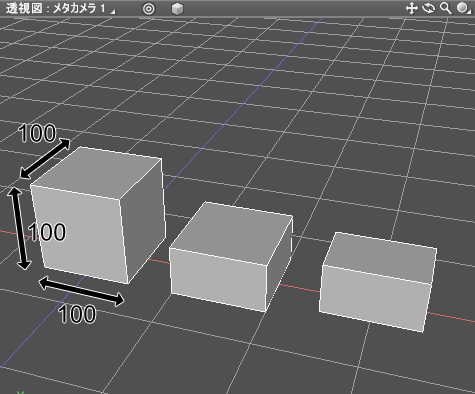
直方体は、XYZ方向の3つの辺の長さで指定されます。
球
中心から一定の距離(半径)でぐるっと全体を囲った形状は「球」になります。
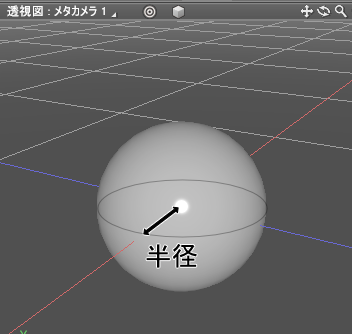
球は、半径で指定されます。
円柱
底面が円で、垂直に高さを持つ形状を「円柱」と呼びます。
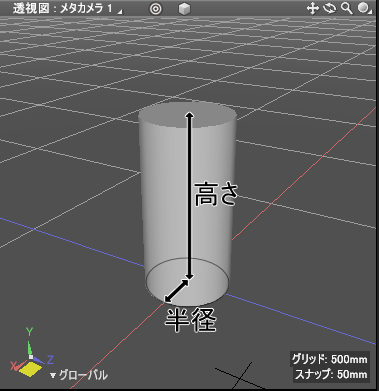
円柱は、底面の円の半径と垂直方向の高さで指定されます。
四角錐 (しかくすい)
底面が四角形で、底面の中心から垂直方向に行くにつれて小さく一点になる形状を「四角錐 (しかくすい)」と呼びます。
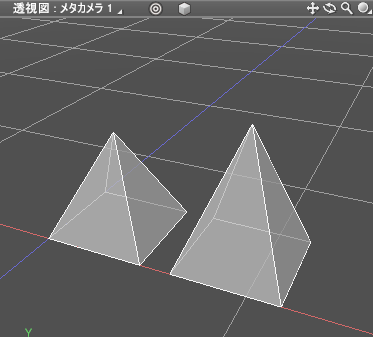
この場合、側面は二等辺三角形になります。
四角錐は、底面の四角形を構成する2辺の長さと垂直方向の高さで指定されます。
円錐 (えんすい)
底面が円で、底面の中心から垂直方向に行くにつれて小さく一点になる形状を「円錐 (えんすい)」と呼びます。
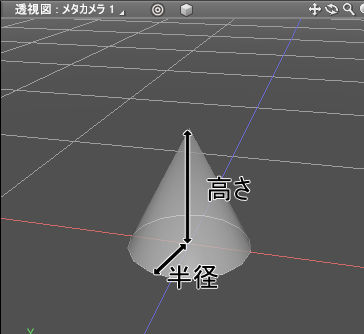
円錐は、底面の円の半径と垂直方向の高さで指定されます。
ブロックUIプログラミングツールで立体を置いてみよう
それでは、ブロックUIプログラミングツールを使ってシーンに立体を配置してみましょう。
ブロックUIプログラミングツールのツールボックスで「形状」を選択。
「直方体の作成」を選択します。
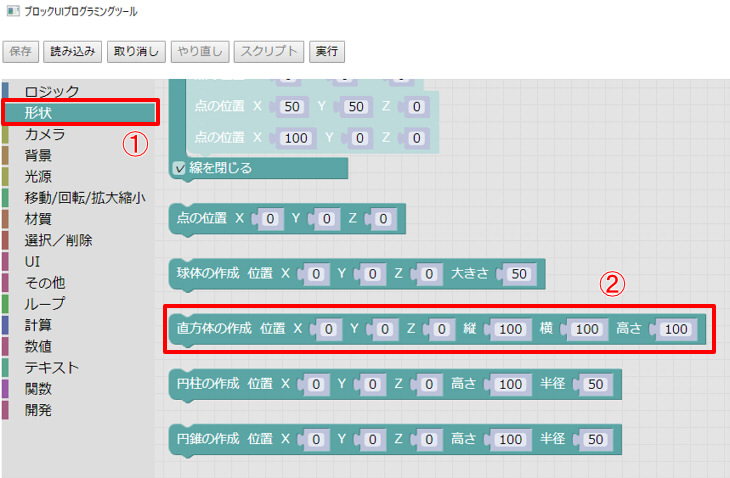
位置(0, 0, 0)、縦100、横100、高さ100の状態で「実行」ボタンを押すと以下のようになります。
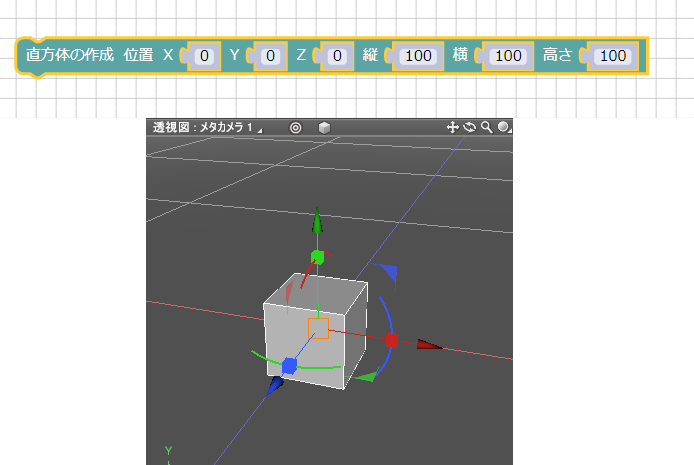
この場合、立方体の中心が原点に来ています。
[問題 2] 一辺が100(mm)の立方体を配置するときに、以下のように底面の頂点が原点に来るように配置しましょう。
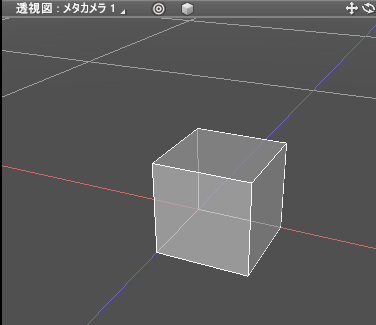
[答え 2] 位置(50, 50, 50)として立方体を配置します。

立方体の中心が原点に来ている場合、各辺の大きさの半分だけずらすことで頂点位置を原点にすることができます。
次に、円錐を配置します。
ブロックUIプログラミングツールのツールボックスで「形状」を選択。
「円錐の作成」を選択します。
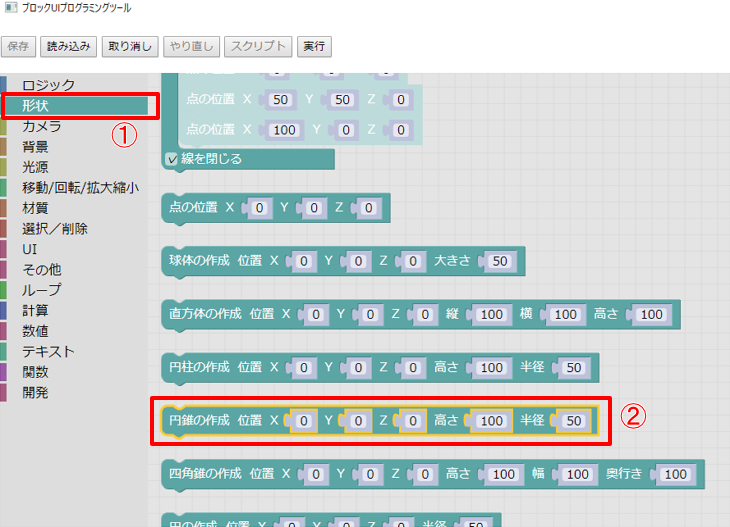
位置(0, 0, 0)、高さ100、半径50の状態で「実行」ボタンを押すと以下のようになります。
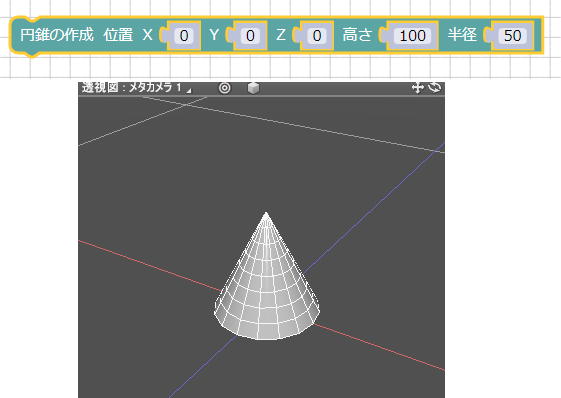
円錐の場合は、底面の中心が原点にきています。
[問題 3] 原点位置を底面の中心として、以下のような形状を作ってみましょう。
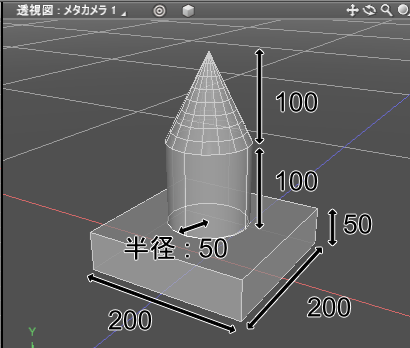
[答え 3] ブロックUIプログラミングツールでは以下のようになります。
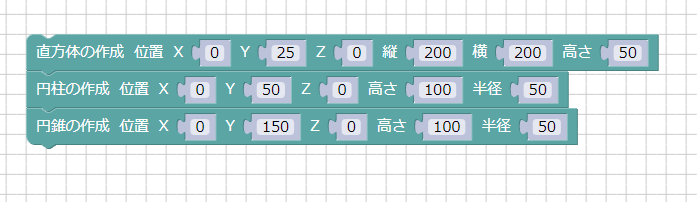
複数の形状が重ねられている場合は、まず何の形状で構成されるかを考えていく必要があります。
一番下は直方体、その上に円柱、さらにその上に同じ半径で円錐を配置しています。
直方体は底面の大きさが200 x 200、高さは50となっています。
また、原点は底面の中心です。
これより、直方体は位置(0, 25, 0)、底面の縦と横は200、高さ50で配置します。
25は「50 ÷ 2」で計算できます。
円柱は50だけ上に配置するため、位置(0, 50, 0)、半径は指定の50、高さは100で配置します。
円錐は50+100の高さに配置するため、位置(0, 150, 0)、半径は50、高さは100で配置します。
原点の高さから順番に積み上げていく場合の足し算や同一半径でつなげる、といったパズル的な要素も入っています。
この形状は簡単な積み木のような組み合わせですが、実際の3Dで形状を作成するという工程(モデリングと呼びます)でも、
このような「分解」する作業は発生します。
今回はここまでです。
立体までいくと必要な知識量も増えますが、表現できることも増えていくのが確認できます。
逆に考えると、表現をより豊かにしていくためには知識を身に着けていく必要がある、というのが理解できるかもしれません。
次回は、今回単語だけ出した「小数」について、円を表現する際の円周率について説明していく予定です。